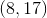All ISEE Lower Level Quantitative Resources
Example Questions
Example Question #294 : Coordinate Geometry
What coordinate point is the blue circle on?

To find the location on a coordinate plane we first look at the 



The blue circle is over 



Example Question #291 : Coordinate Geometry
What coordinate point is the red circle on?

To find the location on a coordinate plane we first look at the 



The red circle is over 



Example Question #51 : Graphing
What coordinate point is the red circle on?

To find the location on a coordinate plane we first look at the 



The red circle is over 



Example Question #313 : Coordinate Geometry
What coordinate point is the purple circle on?

To find the location on a coordinate plane we first look at the 



The purple circle is over 



Example Question #1 : How To Find A Square On A Coordinate Plane

Square ABCD has coordinate points: 









To find the area of square 


Thus, the solution is:
Example Question #2 : How To Find A Square On A Coordinate Plane

Square 





In order to find the perimeter of square 


The solution is:
Example Question #1 : How To Find A Square On A Coordinate Plane

Square 





In order to find the perimeter of square 


Since, 
Example Question #4 : How To Find A Square On A Coordinate Plane

Square 


In order to find the perimeter of square 


Since, 

Example Question #2 : How To Find A Square On A Coordinate Plane
Square 










The area of square 
The solution is:
width 

Example Question #1 : How To Find A Square On A Coordinate Plane
Square 










The fomula used to find the area of a square is
To find the side length of our square look at the distance between the x or y values two of our coordinate points.

Thus, the correct answer is:
Certified Tutor
Certified Tutor
All ISEE Lower Level Quantitative Resources