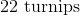We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Lower Level Quantitative : Algebraic Concepts

Study concepts, example questions & explanations for ISEE Lower Level Quantitative

Create An Account

All ISEE Lower Level Quantitative Resources

20 Diagnostic Tests 114 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #51 : Algebraic Concepts

What is the value of the expression?

(5+3) * 2

Possible Answers:

Correct answer:

Explanation:

First you add what is inside the parentheses.

5+3=8 .

Then, we multiply,

8*2 .

This leaves us with our answer of 16.

Report an Error

Example Question #52 : Algebraic Concepts

A pencil costs $1.03 and Elena wants to purchase 386 pencils. Which expression gives the best estimate of the total cost of Alex's purchase in dollars?

Possible Answers:

1*40

130*100

1*400

10*380

130*400

Correct answer:

1*400

Explanation:

To solve, we round $1.03 to $1.00 and round 386 pencils to 400.

Then we would multiply to find the answer, so 1*400 would give us the best estimate.

Report an Error

Example Question #53 : Algebraic Concepts

Find the value of the expression.

(8-6)/2

Possible Answers:

Correct answer:

Explanation:

To solve the expression, you must first solve inside the parentheses, so

8-6=2 .

Then we divide 2 by 2 and are left with our answer, 1.

Report an Error

Example Question #54 : Equations

Caitlin received $\small x$ tickets to a concert for Friday night. She divides them equally among herself and her four friends. Which of the following expressions shows the number of tickets each person received?

Possible Answers:

$\frac{x}{5}$

x-5

$x\cdot 5$

$\frac{x}{4}$

x-4

Correct answer:

$\frac{x}{5}$

Explanation:

Including Caitlin, there are 5 total people receiving tickets.

If she is going to divide them among her friends, then we would use division,

$\frac{\text{Number of Tickets}}{\text{Number of People}}=\frac{x}{5}$

Report an Error

Example Question #55 : Equations

Solve for $\small x$ .

$\small 4x+2x-x=15$

Possible Answers:

$\small x=3$

$\small x=2$

$\small x=5$

$\small x=1$

$\small x=4$

Correct answer:

$\small x=3$

Explanation:

First we add and are left with

$\small 6x-x=15$ .

Then we subtract and are left with

$\small 5x=15$ .

Finally, in order to get the $\small x$ alone, we divide each side by 5 and are left with

$\small x=3$ .

Report an Error

Example Question #54 : Equations

Solve for $\small x$ .

$\small \small 1+3+(8-2)*2=x$

Possible Answers:

$\small x=16$

$\small x=12$

$\small x=19$

$\small x=20$

$\small x=13$

Correct answer:

$\small x=16$

Explanation:

Following the order of operations, we must do the work inside the parentheses first, so we are left with

$\small 1+3+6*2=x$ .

Then we must multiply and are left with

$\small 1+3+12=x$ .

Finally

$\small 4+12=x$ .

$\small x=16$ .

Report an Error

Example Question #54 : Algebraic Concepts

Five more than a number is equal to $\frac{3}{5}$ of twenty-five . What is the number?

Possible Answers:

Correct answer:

Explanation:

From the question, we know that plus a number equals $\frac{3}{5}$ of . In order to find out what $\frac{3}{5}$ of is, multiply $\frac{3}{5}$ by $\frac{25}{1}$ .

$\frac{3}{5}\times\frac{25}{1}=\frac{75}{5}$ , or .

The number we are looking for needs to be five less than , or .

You can also solve this algebraically by setting up this equation and solving:

$5+x=\frac{3}{5}\times25$

5+x=15

Subtract from both sides of the equation.

x=10

Report an Error

Example Question #55 : Algebraic Concepts

Solve for :

14x - 6=64

Possible Answers:

Correct answer:

Explanation:

To solve an equation, first combine like terms. Move the over to the other side of the equation by adding :

14x - 6=64

+6=+6

14x=70

Next, remove the from the variable by dividing by .

$\frac{14x}{14}=\frac{70}{14}\rightarrow x=5$

The answer is .

Report an Error

Example Question #42 : Grade 6

At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade turnips for ears of corn. If a man has ears of corn, then how many turnips can he get?

Possible Answers:

$93\ \text{turnips}$

$39\ \text{turnips}$

$22\ \text{turnips}$

$43\ \text{turnips}$

$94\ \text{turnips}$

Correct answer:

$39\ \text{turnips}$

Explanation:

Ratios can be written in the following format:

$A:B\rightarrow \frac{A}{B}$

Using this format, substitute the given information to create a ratio.

$3\ \text{corn}: 13\ \text{turnips}$

Rewrite the ratio as a fraction.

$3\ \text{corn}: 13\ \text{turnips}\rightarrow \frac{3\ \text{corn}}{13\ \text{turnips}}$

We know that the farmer has ears of corn. Create a ratio with the variable that represents how many turnips he can get.

$\frac{9\ \text{corn}}{T}$

Create a proportion using the two ratios.

$\frac{3\ \text{corn}}{13\ \text{turnips}}=\frac{9\ \text{corn}}{T}$

Cross multiply and solve for .

$9\ \text{corn}\times 13\ \text{turnips}=3\ \text{corn}\times T$

Simplify.

3T=117

Divide both sides of the equation by .

$\frac{3T}{3}=\frac{117}{3}$

Solve.

T=39

The farmer can get $39\ \text{turnips}$ .

Report an Error

Example Question #43 : Grade 6

At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade turnips for ears of corn. If a man has ears of corn, then how many turnips can he get?

Possible Answers:

$171\ \text{turnips}$

$111\ \text{turnips}$

$87\ \text{turnips}$

$127\ \text{turnips}$

$117\ \text{turnips}$

Correct answer:

$117\ \text{turnips}$

Explanation:

Ratios can be written in the following format:

$A:B\rightarrow \frac{A}{B}$

Using this format, substitute the given information to create a ratio.

$3\ \text{corn}: 13\ \text{turnips}$

Rewrite the ratio as a fraction.

$3\ \text{corn}: 13\ \text{turnips}\rightarrow \frac{3\ \text{corn}}{13\ \text{turnips}}$

We know that the farmer has ears of corn. Create a ratio with the variable that represents how many turnips he can get.

$\frac{27\ \text{corn}}{T}$

Create a proportion using the two ratios.

$\frac{3\ \text{corn}}{13\ \text{turnips}}=\frac{27\ \text{corn}}{T}$

Cross multiply and solve for .

$27\ \text{corn}\times 13\ \text{turnips}=3\ \text{corn}\times T$

Simplify.

3T=351

Divide both sides of the equation by .

$\frac{3T}{3}=\frac{351}{3}$

Solve.

T=117

The farmer can get $117\ \text{turnips}$ .

Report an Error

View Tutors

Gabby
Certified Tutor

University of Oregon, Bachelor in Arts, Journalism. University of Oregon, Current Grad Student, Communication, General.

View Tutors

Crystal
Certified Tutor

SUNY at Binghamton, Bachelor of Science, Mechanical Engineering.

View Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

All ISEE Lower Level Quantitative Resources

20 Diagnostic Tests 114 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

LSAT Tutors in Dallas Fort Worth, SAT Tutors in Chicago, Algebra Tutors in Chicago, Reading Tutors in Philadelphia, ACT Tutors in Denver, French Tutors in San Francisco-Bay Area, Biology Tutors in Phoenix, Calculus Tutors in Los Angeles, Algebra Tutors in Miami, French Tutors in Houston

Popular Courses & Classes

Spanish Courses & Classes in Houston, SAT Courses & Classes in Philadelphia, ISEE Courses & Classes in San Diego, MCAT Courses & Classes in Denver, Spanish Courses & Classes in Phoenix, SSAT Courses & Classes in Denver, GRE Courses & Classes in Houston, GMAT Courses & Classes in Los Angeles, Spanish Courses & Classes in Denver, SAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

ISEE Test Prep in Denver, ISEE Test Prep in Boston, ACT Test Prep in Houston, GRE Test Prep in Washington DC, GRE Test Prep in Chicago, SAT Test Prep in Boston, SSAT Test Prep in Denver, SAT Test Prep in New York City, ACT Test Prep in New York City, GRE Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Lower Level Quantitative : Algebraic Concepts

Study concepts, example questions & explanations for ISEE Lower Level Quantitative

All ISEE Lower Level Quantitative Resources

Example Questions

Example Question #51 : Algebraic Concepts

Example Question #52 : Algebraic Concepts

Example Question #53 : Algebraic Concepts

Example Question #54 : Equations

Example Question #55 : Equations

Example Question #54 : Equations

Example Question #54 : Algebraic Concepts

Example Question #55 : Algebraic Concepts

Example Question #42 : Grade 6

Example Question #43 : Grade 6

All ISEE Lower Level Quantitative Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: