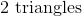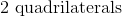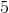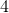ISEE Lower Level Math : Plane Geometry
Study concepts, example questions & explanations for ISEE Lower Level Math
All ISEE Lower Level Math Resources
Example Questions
Example Question #371 : Plane Geometry
Find the length of one side of an equilateral triangle that has a perimeter of 27cm.
The formula to find perimeter of an equilateral triangle is
where a is the length of one side. We can multiply that by 3, because an equilateral triangle has 3 equal sides. Now, to find the length of one side, we will solve for a.
So, we know the perimeter of the equilateral triangle is 27cm. Knowing this, we can substitute. We get
Therefore, the length of one side of the equilateral triangle is 9cm.
Example Question #372 : Plane Geometry
Use the following triangle to answer the question:
Find the perimeter.
To find the perimeter of a triangle, we will use the following formula:
where a, b, and c are the lengths of the sides of the triangle.
Now, given the triangle
we can see that it has sides of length 8ft, 4ft, and 7ft. So, we get
Example Question #1321 : Isee Lower Level (Grades 5 6) Mathematics Achievement
An equilateral triangle has a perimeter of 42 cm. What is the length of one of its sides?
By definition, an equilateral triangle is a triangle with three equal sides. That is, the length of each side of the triangle is going to be the same.
In this problem, we know that the perimeter (the sum of all the lengths) is 42 cm.
Side 1 + Side 2 + Side 3 = 42 cm.
Since the sides are equal, we can write the following equation. 
To find the length of one side of the triangle, we would then divide 3 from both sides.
Example Question #1 : Lines
There is a four sided figure in which none of the lines run parallel to each other. Which of the following could be the appropriate term to describe the figure?
Trapezoid
Parallelogram
None of these
Rectangle
Quadrilateral
Quadrilateral
A key characteristic of a rectangle, parallelogram, and trapezoid is the fact that they each have at least one pair of lines that run parallel to each other. The only option that has lines that may not run parallel to each other is the quadrilateral, which must simply have four sides but has no specifications about parallelism.
Example Question #1 : How To Find Symmetry
If a diagonal is drawn from one corner of a rectangle to the opposite corner, what 2 shapes result?
While drawing a line across a rectangle (so that it bisects 2 sides) can result in 2 quadrilaterals, squares, or rectangles, a line drawn from one corner to the furthest corner results in two triangles. Therefore, the correct answer choice is 2 triangles.
Example Question #2 : How To Find Symmetry
How many lines of symmetry are there in a square?
A line of symmetry is a line that divides a polygon in half and each half is a mirror image of the other. In other words, you can fold the polygon over the symmetry line and each half matches up perfectly.
For a square there are four lines of symmetry. Two are from the diagonals of the square and two are from connecting the midpoints of the opposite sides.
Example Question #1322 : Isee Lower Level (Grades 5 6) Mathematics Achievement
What is the distance between 
The distance formula is 
Let 
Example Question #1331 : Isee Lower Level (Grades 5 6) Mathematics Achievement
What is the distance between 
The distance formula is given by
Let 
Example Question #1332 : Isee Lower Level (Grades 5 6) Mathematics Achievement
What is the distance between 
The distance formula is given by 
Let 
Example Question #1333 : Isee Lower Level (Grades 5 6) Mathematics Achievement
What is the distance between the points 
The distance formula is 
Let 
Plug these two points into the distance formula:
All ISEE Lower Level Math Resources
