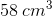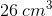All Intermediate Geometry Resources
Example Questions
Example Question #11 : How To Find The Surface Area Of A Prism
Find the surface area of the regular hexagonal prism.


In order to find the surface area, you will need to add up the areas of each face of the prism.
This hexagonal prism has two regular hexagons as its bases.
Recall how to find the area of a regular hexagon:
Now, since we have two hexagons, we can multiply the area by 
Next, this prism has 
Recall how to find the area of a rectangle:
In this prism, the length is also the side of the hexagon, and the width of the rectangle is the height of the prism.
Now, multiply the area of the rectangle by 
Add together the area of the sides and of the bases to find the surface area of the prism.
Plug in the given values to find the surface area of the prism.
Make sure to round to 
Example Question #12 : How To Find The Surface Area Of A Prism
Find the surface area of the regular hexagonal prism.


In order to find the surface area, you will need to add up the areas of each face of the prism.
This hexagonal prism has two regular hexagons as its bases.
Recall how to find the area of a regular hexagon:
Now, since we have two hexagons, we can multiply the area by 
Next, this prism has 
Recall how to find the area of a rectangle:
In this prism, the length is also the side of the hexagon, and the width of the rectangle is the height of the prism.
Now, multiply the area of the rectangle by 
Add together the area of the sides and of the bases to find the surface area of the prism.
Plug in the given values to find the surface area of the prism.
Make sure to round to 
Example Question #13 : How To Find The Surface Area Of A Prism
Find the surface area of the regular hexagonal prism.


In order to find the surface area, you will need to add up the areas of each face of the prism.
This hexagonal prism has two regular hexagons as its bases.
Recall how to find the area of a regular hexagon:
Now, since we have two hexagons, we can multiply the area by 
Next, this prism has 
Recall how to find the area of a rectangle:
In this prism, the length is also the side of the hexagon, and the width of the rectangle is the height of the prism.
Now, multiply the area of the rectangle by 
Add together the area of the sides and of the bases to find the surface area of the prism.
Plug in the given values to find the surface area of the prism.
Make sure to round to 
Example Question #21 : Prisms
Find the surface area of the regular hexagonal prism.


In order to find the surface area, you will need to add up the areas of each face of the prism.
This hexagonal prism has two regular hexagons as its bases.
Recall how to find the area of a regular hexagon:
Now, since we have two hexagons, we can multiply the area by 
Next, this prism has 
Recall how to find the area of a rectangle:
In this prism, the length is also the side of the hexagon, and the width of the rectangle is the height of the prism.
Now, multiply the area of the rectangle by 
Add together the area of the sides and of the bases to find the surface area of the prism.
Plug in the given values to find the surface area of the prism.
Make sure to round to 
Example Question #22 : Prisms
Find the surface area of the regular hexagonal prism.


In order to find the surface area, you will need to add up the areas of each face of the prism.
This hexagonal prism has two regular hexagons as its bases.
Recall how to find the area of a regular hexagon:
Now, since we have two hexagons, we can multiply the area by 
Next, this prism has 
Recall how to find the area of a rectangle:
In this prism, the length is also the side of the hexagon, and the width of the rectangle is the height of the prism.
Now, multiply the area of the rectangle by 
Add together the area of the sides and of the bases to find the surface area of the prism.
Plug in the given values to find the surface area of the prism.
Make sure to round to 
Example Question #23 : Prisms
Find the surface area of the regular hexagonal prism.


In order to find the surface area, you will need to add up the areas of each face of the prism.
This hexagonal prism has two regular hexagons as its bases.
Recall how to find the area of a regular hexagon:
Now, since we have two hexagons, we can multiply the area by 
Next, this prism has 
Recall how to find the area of a rectangle:
In this prism, the length is also the side of the hexagon, and the width of the rectangle is the height of the prism.
Now, multiply the area of the rectangle by 
Add together the area of the sides and of the bases to find the surface area of the prism.
Plug in the given values to find the surface area of the prism.
Make sure to round to 
Example Question #24 : Prisms
Find the surface area of the regular hexagonal prism.


In order to find the surface area, you will need to add up the areas of each face of the prism.
This hexagonal prism has two regular hexagons as its bases.
Recall how to find the area of a regular hexagon:
Now, since we have two hexagons, we can multiply the area by 
Next, this prism has 
Recall how to find the area of a rectangle:
In this prism, the length is also the side of the hexagon, and the width of the rectangle is the height of the prism.
Now, multiply the area of the rectangle by 
Add together the area of the sides and of the bases to find the surface area of the prism.
Plug in the given values to find the surface area of the prism.
Make sure to round to 
Example Question #1 : How To Find The Volume Of A Prism
A prism with a square base has a height of 
If the edge of the base is 
The volume of a prism is given as
where
B = Area of the base
and
h = height of the prism.
Because the base is a square, we have
So plugging in the value of B that we found and h that was given in the problem we get the volume to be the following.
Example Question #61 : Geometry
A rectangular prism has the dimensions of 


The volume of a rectangular prism is given by the following equation:
In this equation, 


The given information does not explicitly state which side each dimension measurement correlates to on the prism. Volume simply requires the multiplication of the dimensions together.
Volume can be solved for in the following way:
Example Question #62 : Geometry
Find the volume of a rectangular prism with a width of 


The volume of a rectangular prism is given by the following equation:
In this equation, 


Because all the necessary information has been provided to solve for the volume, all that needs to be done is substituting in the values for the variables.
Therefore:
All Intermediate Geometry Resources