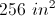We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : Parallelograms

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : How To Find The Length Of The Side Of A Parallelogram

Given that a parallelogram has a height of 2.5ft and an area of 20ft^2 . Find the base of the parallelogram.

Possible Answers:

12ft

7.5ft

6.5ft

8ft

Correct answer:

8ft

Explanation:

In order to find the base of this parallelogram apply the formula: $Area=base\times height$

Thus, the solution is:

$20=base\times2.5$

$base=\frac{20}{2.5}$

base=8

Report an Error

Example Question #2 : How To Find The Length Of The Side Of A Parallelogram

Given: Quadrilateral ABCD with diagonal $\overline{AC}$ ; $\bigtriangleup ABC \cong \bigtriangleup CDA$ .

True or false: From the information given, it follows that Quadrilateral ABCD is a parallelogram.

Possible Answers:

False

True

Correct answer:

True

Explanation:

Corresponding parts of congruent triangles are, by definition, congruent. Thus, from the statement $\bigtriangleup ABC \cong \bigtriangleup CDA$ , it follows that:

$\overline{AB} \cong \overline{CD}$ and $\overline{BC} \cong \overline{DA}$

Quadrilateral ABCD therefore has two sets of congruent opposite sides. This is a sufficient condition for the quadrilateral to be a parallelogram.

Report an Error

Example Question #3 : How To Find The Length Of The Side Of A Parallelogram

Quadrilateral ABCD is both a rhombus and a rectangle.

True or false: Quadrilateral ABCD must be a square.

Possible Answers:

False

True

Correct answer:

True

Explanation:

A rhombus is defined to be a parallelogram with four congruent sides; a rectangle is defined to be a parallelogram with four right angles.

A square is defined to be a parallelogram with four congruent sides and four right angles. If a parallelogram is both a rhombus and a rectangle, then it fits both characteristics and is therefore a square.

Report an Error

Example Question #1 : How To Find The Area Of A Parallelogram

The perimeter of a square is $24\; in$ . If the sides of the square are reduced by a factor of two, what is the area of the new square?

Possible Answers:

$36\; in^{2}$

$27\; in^{2}$

$45\; in^{2}$

$18\; in^{2}$

$9\; in^{2}$

Correct answer:

$9\; in^{2}$

Explanation:

The perimeter of a square is geven by P=4s and the area of a square is given by $A=s^{2}$ .

Thus $P=4s=24\: in$

so $s=6\; in$ .

The original side is reduced by a factor of which results in a new side of $3\; in$ . The area of the new square is geven by

$A=s^{2}=3^{2}=9\; in^{2}$

Report an Error

Example Question #2 : How To Find The Area Of A Parallelogram

Find the area of the box in square inches:

Geo_box

Possible Answers:

2x + 2y + 38

x + y + 19

xy + 7x + 12y +84

84xy

12x +7y

Correct answer:

xy + 7x + 12y +84

Explanation:

The answer is xy + 7x + 12y +84 . You can find the area of this box by multiplying the length by its width:

Foil (12 + x) (7 + y ) = xy + 7x + 12y +84

If you chose 2x + 2y + 38 , you added the sides to get the perimeter.

Just remember, the width is 12 added to . Not 12 times the side of .

Report an Error

Example Question #2 : How To Find The Area Of A Parallelogram

If all angles are right angles in the figure below, what is the total area of the figure?

Box1

Possible Answers:

$184\ in^{2}$

$152\ in^{2}$

$256\ in^{2}$

$308\ in^{2}$

$164\ in^{2}$

Correct answer:

$164\ in^{2}$

Explanation:

The answer is $164\ in^{2}$ .

To get the area, you would need to find the missing sides. Since the horizontal top is 8+8=16 inches total, the bottom must be inches total. Thus you would subtract 16-6 to get for the missing bottom horizontal side.

The vertical right side is 4+12 = 16 inches total. Then you would subtract 16-10 to get for the missing vertical side.

Then you would have to split the figure into 3 different boxes and find the area of each one. Then you would add the area of each box

$(32+60+72)=164\ in ^{2}$

Report an Error

Example Question #1 : How To Find The Area Of A Parallelogram

What is the area of a parallelogram if the base is $1.5\:cm$ , and the height is $1.0\:cm$ ?

Possible Answers:

$0.25\:cm$

$0.75\:cm$

$3\:cm$

$1.5\sqrt2\:cm$

$1.5\:cm$

Correct answer:

$1.5\:cm$

Explanation:

The formula for the area of a parallelogram is:

$A=base\cdot height$

So, we are given all of the information that we need to solve this problem. Substitute the provided values into the equation and simplify:

$A= (1.5\:cm)(1\:cm) =1.5\:cm^2$

Report an Error

Example Question #5 : How To Find The Area Of A Parallelogram

What is the area of a parallelogram if the base is $2x\:cm$ and the height is $x^2\:cm$ ?

Possible Answers:

$2x^3\:cm^2$

$x^3\:cm^2$

$2x+x^2\:cm^2$

$2\sqrt2x^3\:cm^2$

$2x^2\:cm^2$

Correct answer:

$2x^3\:cm^2$

Explanation:

The formula for the area of a parallelogram is:

$A=base\cdot height$

Substitute in the provided values and simplify to calculate the correct answer:

$A= (2x\:cm)(x^2\:cm) =2x^3\:cm^2$

Report an Error

Example Question #6 : How To Find The Area Of A Parallelogram

Find the area of a parallelogram if the base is (x-2) and the height is (x+4) .

Possible Answers:

x^2+2x-8

4x+4

2x+2

x^2-2x-8

x^2-8

Correct answer:

x^2+2x-8

Explanation:

The formula for the area of a parallelogram is:

$A=base\cdot height$

Substitute the values provided in the question:

A= (x-2)(x+4)

Use the FOIL method to simplify:

A=(x)(x)+(x)(4) +(-2)(x)+(-2)(4)

A= x^2+4x-2x-8

A=x^2+2x-8

Report an Error

Example Question #3 : How To Find The Area Of A Parallelogram

What is the area of a parallelogram if the base is $\sqrt2\:cm$ and the height is $\sqrt3\:cm$ ?

Possible Answers:

$\frac{\sqrt6}{2}\:cm^2$

$\frac{\sqrt5}{2}\:cm^2$

$\sqrt5\:cm^2$

$\sqrt6\:cm^2$

$\sqrt2 + \sqrt3\:cm^2$

Correct answer:

$\sqrt6\:cm^2$

Explanation:

The formula for the area of a parallelogram is:

$A=base\cdot height$

Substitute the values provided in the problem and solve to calculate the correct answer:

$A= (\sqrt2\:cm)(\sqrt3\:cm) =\sqrt6\:cm^2$

Report an Error

View Tutors

Adair
Certified Tutor

Marymount College, Bachelor of Science, Chemistry.

View Tutors

Paarth
Certified Tutor

New Jersey Institute of Technology, Bachelor of Science, Computer Science.

View Tutors

Joshua
Certified Tutor

Murray State University, Bachelor in Arts, Spanish. Lipscomb University, Bachelor of Science, Teacher Assistant.

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Houston, SAT Tutors in Seattle, Chemistry Tutors in Seattle, Algebra Tutors in San Francisco-Bay Area, Spanish Tutors in Atlanta, Spanish Tutors in Denver, Calculus Tutors in Philadelphia, Reading Tutors in Boston, French Tutors in Seattle, Spanish Tutors in Philadelphia

Popular Courses & Classes

ISEE Courses & Classes in Philadelphia, SAT Courses & Classes in Boston, GRE Courses & Classes in Philadelphia, LSAT Courses & Classes in Miami, GMAT Courses & Classes in Atlanta, GRE Courses & Classes in Atlanta, GRE Courses & Classes in Chicago, MCAT Courses & Classes in Chicago, ISEE Courses & Classes in Chicago, GRE Courses & Classes in Dallas Fort Worth

Popular Test Prep

MCAT Test Prep in San Francisco-Bay Area, ACT Test Prep in Houston, GMAT Test Prep in Atlanta, GRE Test Prep in Boston, SAT Test Prep in Houston, GMAT Test Prep in Philadelphia, GRE Test Prep in Chicago, LSAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Philadelphia, SSAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : Parallelograms

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #2 : How To Find The Length Of The Side Of A Parallelogram

Example Question #2 : How To Find The Length Of The Side Of A Parallelogram

Example Question #3 : How To Find The Length Of The Side Of A Parallelogram

Example Question #1 : How To Find The Area Of A Parallelogram

Example Question #2 : How To Find The Area Of A Parallelogram

Example Question #2 : How To Find The Area Of A Parallelogram

Example Question #1 : How To Find The Area Of A Parallelogram

Example Question #5 : How To Find The Area Of A Parallelogram

Example Question #6 : How To Find The Area Of A Parallelogram

Example Question #3 : How To Find The Area Of A Parallelogram

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: