All Intermediate Geometry Resources
Example Questions
Example Question #1 : How To Find An Angle In A Hexagon
What is the interior angle of a regular hexagon if the area is 15?
The area has no relevance to find the angle of a regular hexagon.
There are 6 sides in a regular hexagon. Use the following formula to determine the interior angle.
Substitute 
Since there are 6 sides, divide this number by 6 to determine the value of each interior angle.
Example Question #1 : How To Find An Angle In A Hexagon
Given: Regular Hexagon 




True or false: Quadrilateral 
True
False
False
Below is regular Hexagon 



Each angle of a regular hexagon measures 

The angles of a rectangle must measure 

Example Question #91 : Hexagons
True or false: Each of the six angles of a regular hexagon measures 
True
False
True
A regular polygon with 

Setting 
The statement is therefore true.
Example Question #901 : Plane Geometry
True or false: Each of the exterior angles of a regular hexagon measures 
True
False
False
If one exterior angle is taken at each vertex of any polygon, and their measures are added, the sum is 

Solve for 
The statement is false.
Example Question #6 : How To Find An Angle In A Hexagon
Given: Hexagon 
True, false, or undetermined: Hexagon 
True
False
Undetermined
False
Suppose Hexagon 

A hexagon has 6 sides, so set 
Since one angle is given to be of measure 
Example Question #91 : Hexagons
What is the measure of one exterior angle of a regular twenty-sided polygon?
The sum of the exterior angles of any polygon, one at each vertex, is 

Example Question #8 : How To Find An Angle In A Hexagon
Which of the following cannot be the six interior angle measures of a hexagon?
All of these can be the six interior angle measures of a hexagon.
All of these can be the six interior angle measures of a hexagon.
The sum of the interior angle measures of a hexagon is
Add the angle measures in each group.
In each case, the angle measures add up to 720, so the answer is that all of these can be the six interior angle measures of a hexagon.
Example Question #1 : How To Find The Area Of A Hexagon
An equilateral hexagon has sides of length 6, what is it's area?
An equilateral hexagon can be divided into 6 equilateral triangles of side length 6.
The area of a triangle is 




Example Question #91 : Hexagons
What is the area of a regular hexagon with a long diagonal of length 12?

A regular hexagon can be divided into 12 30-60-90 right triangles with hypotenuse equal to the length of half of a diagonal, or 6 in this case (see image). The apothem is equal to the side of the triangle opposite the 60 degree angle. Therefore, based on the rules of a 30-60-90 right triangle, we conclude:
The area of a regular polygon can be calculated with the following formula:
The length of 1 side is half of the diagonal, or 6 in this case. The perimeter is the sum of lengths of the sides.
Therefore the area is equal to:
Example Question #1 : How To Find The Area Of A Hexagon
A single hexagonal cell of a honeycomb is two centimeters in diameter.

What’s the area of the cell to the nearest tenth of a centimeter?
Cannot be determined
How do you find the area of a hexagon?
There are several ways to find the area of a hexagon.
- In a regular hexagon, split the figure into triangles.
- Find the area of one triangle.
- Multiply this value by six.
Alternatively, the area can be found by calculating one-half of the side length times the apothem.
Regular hexagons:
Regular hexagons are interesting polygons. Hexagons are six sided figures and possess the following shape:
In a regular hexagon, all sides equal the same length and all interior angles have the same measure; therefore, we can write the following expression.

One of the easiest methods that can be used to find the area of a polygon is to split the figure into triangles. Let's start by splitting the hexagon into six triangles.

In this figure, the center point, 


We also know the following:
Now, let's look at each of the triangles in the hexagon. We know that each triangle has two two sides that are equal; therefore, each of the base angles of each triangle must be the same. We know that a triangle has 
Each angle in the triangle equals 



Let's solve for the length of this triangle. Remember that in 
Now, we can analyze 


We know the measure of both the base and height of 
Now, we need to multiply this by six in order to find the area of the entire hexagon.
We have solved for the area of a regular hexagon with side length, 
If we are not given a regular hexagon, then we an solve for the area of the hexagon by using the side length(i.e. 



Alternative method:
If we are given the variables 

In this equation, 




Solution:
In the problem we are told that the honeycomb is two centimeters in diameter. In order to solve the problem we need to divide the diameter by two. This is because the radius of this diameter equals the interior side length of the equilateral triangles in the honeycomb. Lets find the side length of the regular hexagon/honeycomb.
Substitute and solve.
We know the following information.
As a result, we can write the following:
Let's substitute this value into the area formula for a regular hexagon and solve.
Simplify.
Solve.
Round to the nearest tenth of a centimeter.
All Intermediate Geometry Resources
































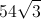

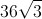


























![\textup{Area of Hexagon}[ABCDEF]=6\times\frac{\sqrt{3}s^2}{4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1065143/gif.latex)
![\textup{Area of Hexagon}[ABCDEF]=\frac{6 \sqrt{3}s^2}{4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1065144/gif.latex)
![\textup{Area of Hexagon}[ABCDEF]=\frac{3\sqrt{3}}{2}\times s^2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1065145/gif.latex)















