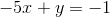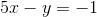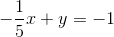Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : Intermediate Geometry

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Equation Of A Curve

If a line's -intercept is . and the -intercept is , what is the equation of the line?

Possible Answers:

-5x+y=-1

$-\frac{1}{5}x+y=\frac{1}{5}$

5x-y=-1

$-\frac{1}{5}x+y=-1$

$\frac{1}{5}x-\frac{1}{5}y=-1$

Correct answer:

$-\frac{1}{5}x+y=-1$

Explanation:

Write the equation in slope-intercept form:

y=mx+b

We were given the -intercept, , which means b=-1 :

y=mx-1

Given the -intercept is , the point existing on the line is (5,0) . Substitute this point into the slope-intercept equation and then solve for to find the slope:

0=m(5)-1

Add to each side of the equation:

1=5m

Divide each side of the equation by :

$m=\frac{1}{5}$

Substituting the value of back into the slope-intercept equation, we get:

$y=\frac{1}{5}x-1$

By subtracting $-\frac{1}{5}x$ on both sides, we can rearrange the equation to put it into standard form:

$-\frac{1}{5}x+y=-1$

Report an Error

Example Question #1 : How To Find The Equation Of A Curve

Find the -intercept of:

y=4x+2

Possible Answers:

x=-2

x=1

x=0.5

x=-0.5

x=2

Correct answer:

x=-0.5

Explanation:

To find the x-intercept, we need to find the value of when y=0 .

So we first set to zero.

y=4x+2

turns into

0=4x+2

Lets subtract from both sides to move to one side of the equation.

-4x=4x-4x+2

After doing the arithmetic, we have

-4x=2 .

Divide by from both sides

$\frac{-4x}{-4}=\frac{2}{-4}$

x=-0.5

Report an Error

Example Question #1 : How To Find The Equation Of A Curve

What is the -intercept of:

y=x^2+x+9

Possible Answers:

y=10

x=9

x=2

y=9

y=-9

Correct answer:

y=9

Explanation:

To find the y-intercept, we set x=0

y=x^2+x+9

turns into

y=0^2+0+9 .

After doing the arithmetic we get

y=9 .

Report an Error

Example Question #2 : How To Find The Equation Of A Curve

What is the -intercept of:

y=3x+3

Possible Answers:

y=1

x=1

x=-1

y=-1

x=0

Correct answer:

x=-1

Explanation:

The x-intercept can be found where y=0

y=3x+3

turns into

0=3x+3 .

Lets subtract from both sides to solve for .

-3x=3x-3x+3

After doing the arithmetic we have

-3x=3 .

Divide both sides by

$\frac{-3x}{-3}=\frac{3}{-3}$

x=-1

Report an Error

Example Question #3 : How To Find The Equation Of A Curve

Suppose two intercepts create a line. If the -intercept is and -intercept is , what is the equation of the line?

Possible Answers:

y=2x+2

$y=-\frac{1}{2}x+2$

y=-2x+2

x-2y=0

$y=\frac{1}{2}x+2$

Correct answer:

y=-2x+2

Explanation:

Rewrite the intercepts in terms of points.

X-intercept of 1: (1,0) .

Y-intercept of 2: (0,2)

Write the slope-intercept form for linear equations.

y=mx+b

Substititute the y-intercept into the slope-intercept equation.

2=m(0)+b

b=2

Substitute both the x-intercept point and the y-intercept into the equation to solve for slope.

0=m(1)+2

-2=m

Rewrite by substituting the values of and into the y-intercept form.

y=-2x+2

Report an Error

Example Question #1 : How To Find The Equation Of A Curve

Which equation has a y-intercept at 2 and x-intercepts at -1 and 6?

Possible Answers:

$\small y = -3(x+1)(x-2)$

$\small y = \frac{-1}{3}(x+1)(x-6)$

$\small y = \frac{1}{3}(x-1)(x+6)$

$\small y=3 (x+1)(x-2 )$

$\small \small y = (x+1)(x-6)$

Correct answer:

$\small y = \frac{-1}{3}(x+1)(x-6)$

Explanation:

In order for the equation to have x-intercepts at -1 and 6, it must have $\small (x+1)$ and (x-6) as factors. This leaves us with only 2 choices, $\small \small y = (x+1)(x-6)$ or $\small y = \frac{-1}{3}(x+1)(x-6)$

This equation must also have a y-intercept of 2. This means that plugging in 0 for x will gives us a y-value of 2. Because we have two options, we could plug in 0 for x in each to see which gives us an answer of 2:

a) $\small y = (0+1)(0-6) = 1*-6 = -6$ we can eliminate that choice

b) $\small y= -\frac{1}{3}(0+1)(0-6) = -\frac{1}{3}*1*-6 = 2$ this must be the right choice.

If we hadn't been given multiple options, we could have set up the following equation to figure out the third factor:

$\small 2 = C(0+1)(0-6)$

$\small 2 = C*1*-6$

$\small 2 = -6C$ divide by -6

$\small -\frac{1}{3} = C$

Report an Error

Example Question #2 : How To Find The Equation Of A Curve

Which equation would have an x-intercept at $\small x=2$ and a y-intercept at $\small y=-3$ ?

Possible Answers:

$y = \frac{2}{3}x - 3$

$\small y = \frac{3}{2}x - 3$

$\small y = \frac{3}{2}x + 3$

$\small y = -\frac{3}{2}x - 3$

$\small y = -\frac{2}{3}x + 2$

Correct answer:

$\small y = \frac{3}{2}x - 3$

Explanation:

We're writing the equation for a line passing through the points $\small (0,-3)$ and $\small (2,0)$ . Since we already know the y-intercept, we can figure out the slope of this line and then write a slope-intercept equation.

To determine the slope, divide the change in y by the change in x:

$\small \frac{-3 - 0 }{ 0 - 2 } = \frac{-3}{-2} = \frac{3}2$

The equation for this line would be $\small y = \frac{3}{2}x - 3$ .

Report an Error

Example Question #2 : How To Find The Equation Of A Curve

Write the equation of a line with intercepts (0, 4) and (-1, 0 )

Possible Answers:

y = 4x + 4

$y = -\frac{1}{4}x + 1$

y = 5x-1

y = -x+5

$y = \frac{1}{4}x +1$

Correct answer:

y = 4x + 4

Explanation:

The line will eventually be in the form y = mx+b where is the y-intercept.

The y-intercept in this case is .

To find the equation, plug in for , and the other point, (-1,0) as x and y:

0 = m(-1)+ 4

0 = -m + 4 add to both sides

m = 4

This means the equation is y = 4x + 4

Report an Error

Example Question #2 : How To Find The Equation Of A Curve

Which equation has the x- and y-intercepts (2,0) and (0,7) ?

Possible Answers:

$y = \frac{2}{7} x + 2$

$y = \frac{7}{2} x +3$

$y = -\frac{2}{7} + 3$

$y = -\frac{7}{2}x + 7$

y = 5x + 1

Correct answer:

$y = -\frac{7}{2}x + 7$

Explanation:

Since this line has the y-intercept (0,7)

, we know that in the form y = mx+b

We can plug in the other intercept's coordinates for

and

to solve for

subtract

divide by

$\frac{-7}{2} = m$

The line is $y = -\frac{7}{2}x + 7$

Report an Error

Example Question #1 : How To Find The Equation Of A Circle

What is the equation for a circle centered at (1,2) with a radius of ?

Possible Answers:

$(x+2)^{2}+ (y+1)^{2} = 36$

$(x+1)^{2}+ (y-2)^{2} = 9$

$(x-2)^{2}+ (y+1)^{2} = 18$

$(x-1)^{2}+ (y+2)^{2} = -9$

$(x-1)^{2}+ (y-2)^{2} = 9$

Correct answer:

$(x-1)^{2}+ (y-2)^{2} = 9$

Explanation:

The general equation for a circle centered at the origin is given by $x^{2}+y^{2}=r^{2}$ where is the radius of the circle.

To translate the origin to the first quadrant we need to subtract the appropriate amount to bring it back to center.

So the equation becomes $(x-1)^{2}+(y-2)^{2}=9$

Report an Error

View Tutors

Kalyani
Certified Tutor

Andhra Loyola College, Bachelor of Science, Mathematics. Krishna University, Master of Science, Mathematics.

View Tutors

Elsa
Certified Tutor

California State University-Fullerton, Bachelor in Business Administration, Finance. National University, Master of Arts Teac...

View Tutors

Gabriel
Certified Tutor

Florida State University, Bachelor in Arts, Writing, General.

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Statistics Tutors in Atlanta, English Tutors in Chicago, Algebra Tutors in Atlanta, SSAT Tutors in Los Angeles, ACT Tutors in San Francisco-Bay Area, Biology Tutors in Miami, SAT Tutors in San Francisco-Bay Area, ISEE Tutors in Washington DC, Reading Tutors in Houston, GRE Tutors in Philadelphia

Popular Courses & Classes

GMAT Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in New York City, GMAT Courses & Classes in Boston, Spanish Courses & Classes in Chicago, ISEE Courses & Classes in Washington DC, MCAT Courses & Classes in Denver, MCAT Courses & Classes in Miami, SAT Courses & Classes in Denver, SSAT Courses & Classes in Miami, GRE Courses & Classes in Chicago

Popular Test Prep

SSAT Test Prep in Boston, SSAT Test Prep in Denver, GMAT Test Prep in San Francisco-Bay Area, ACT Test Prep in Washington DC, SAT Test Prep in Atlanta, ISEE Test Prep in Phoenix, GMAT Test Prep in Boston, GMAT Test Prep in Miami, GRE Test Prep in Phoenix, LSAT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : Intermediate Geometry

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #1 : How To Find The Equation Of A Curve

Example Question #1 : How To Find The Equation Of A Curve

Example Question #1 : How To Find The Equation Of A Curve

Example Question #2 : How To Find The Equation Of A Curve

Example Question #3 : How To Find The Equation Of A Curve

Example Question #1 : How To Find The Equation Of A Curve

Example Question #2 : How To Find The Equation Of A Curve

Example Question #2 : How To Find The Equation Of A Curve

Example Question #2 : How To Find The Equation Of A Curve

Example Question #1 : How To Find The Equation Of A Circle

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: