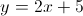Parallel lines will never touch, and therefore they must have the same slope.

Many of the answers are reciprocals or negative slopes, but the slope we are looking for is .

That leaves us with 2 answers. However, one of the answers is the exact same equation for a line as the given equation. Therefore our answer is:

Two lines are perpendicular if and only if their slopes are negative reciprocals. To find the slope, we must put the equation into slope-intercept form,  , where  equals the slope of the line. We begin by subtracting  from each side, giving us . Next, we subtract 32 from each side, giving us . Finally, we divide each side by , giving us . We can now see that the slope is . Therefore, any line perpendicular to  must have a slope of . Of the equations above, only  has a slope of .

Convert the given equation to slope-intercept form: 

Divide both sides of the equation by :

The slope of this function is :  

The slope of the perpendicular line will be the negative reciprocal of the original slope. Substitute and solve:

Only  has a slope of .

Two perpendicular lines have slopes that are opposite reciprocals, meaning that the sign changes and the reciprocal of the slope is taken. 

The original equation is in slope-intercept form,

 where  represents the slope.

In this case, the slope of the original is: 

After taking the opposite reciprocal, the result is the slope below: 

Any equation of the form , such as , can be graphed by a vertical line; any equation of the form , such as , can be graphed  by a horizontal line. A vertical line and a horizontal line are perpendicular to each other.

Write each equation in the slope-intercept form  by solving for ; the -coefficient  is the slope of the line.

Subtract  from both sides:

The line of this equation has slope .

Subtract  from both sides:

Multiply both sides by 

The line of this equation has slope .

Two lines are parallel if and only if they have the same slope; this is not the case. They are perpendicular if and only if the product of their slopes is ; this is not the case, since

.

The correct response is that the lines are neither parallel nor perpendicular.

Write each equation in the slope-intercept form  by solving for ; the -coefficient  is the slope of the line.

Subtract  from both sides:

Multiply both sides by :

The slope is the -coefficient 

Add  to both sides:

Multiply both sides by :

The slope is the -coefficient .

Two lines are parallel if and only if they have the same slope; this is not the case. They are perpendicular if and only if the product of their slopes is ; this is not the case, since . The lines are neither parallel nor perpendicular.

Two lines on the coordinate plane are perpendicular if and only if the product of their slopes is . The product of the slopes of the lines in question is

,

so the lines are indeed perpendicular.

Two lines are perpendicular if and only if the product of their slopes is . The slope of each line can be found from the coordinates of two points using the slope formula

To find the slope of the first line, set :

To find the slope of the second line, set :

The product of the slopes is

As the product is not , the lines are not perpendicular.

Two lines on the coordinate plane are perpendicular if and only if the product of their slopes is . The product of the slopes of the lines in question is

The product is not equal to , so the lines are not perpendicular.