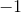Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : Intermediate Geometry

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Equation Of A Perpendicular Line

Suppose a perpendicular line passes through y=2x-1 and point (-1,5) . Find the equation of the perpendicular line.

Possible Answers:

y=-2x-7

y=-2x+3

$y=-\frac{1}{2}x+4\frac{1}{2}$

$y=-\frac{1}{2}x-4\frac{1}{2}$

$y=\frac{1}{2}x+5\frac{1}{2}$

Correct answer:

$y=-\frac{1}{2}x+4\frac{1}{2}$

Explanation:

Find the slope from the given equation y=2x-1 . The slope is: m1=2 .

The slope of the perpendicular line is the negative reciprocal of the original slope.

$m2=-\frac{1}{m1}=-\frac{1}{2}$

Plug in the perpendicular slope and the given point to the slope-intercept equation.

y=mx+b

$5=\left(-\frac{1}{2}\right)(-1)+b$

$5=\frac{1}{2}+b$

$b=4\frac{1}{2}$

Plug in the perpendicular slope and the y-intercept into the slope-intercept equation to get the equation of the perpendicular line.

$y=-\frac{1}{2}x+4\frac{1}{2}$

Report an Error

Example Question #4 : How To Find The Equation Of A Perpendicular Line

Find a line perpendicular y=6x-5 , but passing through the point (7,2) .

Possible Answers:

$y=6x+\frac{19}{6}$

$y=6x-\frac{19}{6}$

$y=\frac{1}{6}x-\frac{19}{6}$

$y=-\frac{1}{6}x+\frac{19}{6}$

$y=-\frac{1}{6}x-\frac{19}{6}$

Correct answer:

$y=-\frac{1}{6}x+\frac{19}{6}$

Explanation:

Since we need a line perpendicular to y=6x-5 we know our slope must be $m=-\frac{1}{6}$ . This is because perpendicular lines have slopes that are negative reciprocals of each other. In order for our new line to pass through the point (7,2) we must use the point slope formula. Be sure to use the perpendicular slope.

$y-y_{1}=m(x-x_{1})$

$y-2=\frac{-1}{6}(x-7)$

$y=\frac{-1}{6}x+\frac{7}{6}+2$

$y=\frac{-1}{6}x+\frac{7}{6}+\frac{12}{6}$

$\mathbf{y=-\frac{1}{6}x+\frac{19}{6}}$

Report an Error

Example Question #7 : How To Find The Equation Of A Perpendicular Line

A line is perpendicular to the line of the equation

5x+ 7y = 32

and passes through the point (-2, 8) .

Give the equation of the line.

Possible Answers:

$\textup{None of the other choices gives the correct response}$

5x- 7y = -66

7x + 5y= 26

7x- 5y= -54

5x+ 7y = 46

Correct answer:

7x- 5y= -54

Explanation:

A line perpendicular to another line will have as its slope the opposite of the reciprocal of the slope of the latter. Therefore, it is necessary to find the slope of the line of the equation

5x+ 7y = 32

Rewrite the equation in slope-intercept form y = mx+ b . , the coefficient of , will be the slope of the line.

Add -5x to both sides:

5x+ 7y + (-5x ) = 32 + (-5x )

7y = -5x+32

Multiply both sides by $\frac{1}{7}$ , distributing on the right:

$\frac{1}{7} \cdot 7y = \frac{1}{7} \cdot( -5x+32)$

$y = -\frac{5}{7}x+\frac{32}{7}$

The slope of this line is $-\frac{5}{7}$ . The slope of the first line will be the opposite of the reciprocal of this, or $\frac{7}{5}$ . The slope-intercept form of the equation of this line will be

$y = \frac{7}{5}x+b$ .

To find , set x = -2 and y = 8 and solve:

$8 = \frac{7}{5} (-2)+b$

$8 = - \frac{14}{5} +b$

$\frac{40}{5} = - \frac{14}{5} +b$

Add $\frac{14}{5}$ to both sides:

$\frac{40}{5} + \frac{14}{5} = - \frac{14}{5} +b + \frac{14}{5}$

$\frac{54}{5} = b$

The equation, in slope-intercept form, is $y = \frac{7}{5}x+ \frac{54}{5}$ .

To rewrite in standard form with integer coefficients:

Multiply both sides by 5:

$5 y =5 \left (\frac{7}{5}x+ \frac{54}{5} \right )$

$5 y =5 \left (\frac{7}{5}x \right ) + 5 \left ( \frac{54}{5} \right )$

5 y =7x+54

Add -5y-54 to both sides:

5 y + (-5y-54) =7x+54 + (-5y-54)

-54 =7x -5y

7x -5y = -54

Report an Error

Example Question #1 : How To Find The Slope Of A Perpendicular Line

Any line that is perpendicular to 18-9y=13x must have a slope of what?

Possible Answers:

-9/13

9/13

13/9

-13/9

1/2

Correct answer:

9/13

Explanation:

Two lines are perpendicular if and only if their slopes are negative reciprocals of each other. To find the slope, we must put the equation into slope-intercept form, y=mx+b , where equals the slope of the line. First, we must subtract from both sides of the equation, giving us -9y=13x-18 . Next, we must divide both sides by , giving us y=-13x/9+2 . We can now see that the slope of this line is -13/9 . Therefore, any line that is perpendicular to this one must have a slope of 9/13 .

Report an Error

Example Question #1 : How To Find The Slope Of A Perpendicular Line

What is the slope of any line perpendicular to $y=-\frac{1}{2}x+5$ ?

Possible Answers:

$-\frac{1}{2}$

$\frac{1}{2}$

Correct answer:

Explanation:

The slope of a perpendicular line is the negative reciprocal of the original slope.

The original slope is $-\frac{1}{2}$ .

The negative reciprocal of the original slope is:

$-\frac{1}{-(\frac{1}{2})} = 2$

Report an Error

Example Question #1 : How To Find The Slope Of A Perpendicular Line

What is the slope of a line perpendicular to x=100 ?

Possible Answers:

$\frac{1}{100}$

100

$-\frac{1}{100}$

Correct answer:

Explanation:

The equation x=100 is a vertical line on the coordinate plane. Any line perpendicular to a vertical line is a horizontal line. Horizontal lines have slopes of zero.

The correct answer is .

Report an Error

Example Question #11 : Perpendicular Lines

Assume the points (1,1) and (2,3) form a line. A perpendicular line is drawn to intersect this line. What is the slope of the perpendicular line?

Possible Answers:

$-\frac{1}{2}$

$\frac{1}{2}$

Correct answer:

$-\frac{1}{2}$

Explanation:

Write the slope formula and find the slope of the first line.

$m=\frac{y_2-y_1}{x_2-x_1}=\frac{3-1}{2-1}=\frac{2}{1}=2$

The slope of the perpendicular line is the negative reciprocal of the original slope.

$-\frac{1}{(2)} =-\frac{1}{2}$

Therefore, the slope of the perpendicular line is $-\frac{1}{2}$ .

Report an Error

Example Question #1 : How To Find The Slope Of A Perpendicular Line

A line goes through the following (4,5) and (10,8) .

Find the slope of a line perpendicular to the line given.

Possible Answers:

1.5

0.5

-0.5

Correct answer:

Explanation:

The slope of a line perpendicular is the negative reciprocal of the given line.

Since the given slope is calculated as $\frac{8-5}{10-4}=\frac{3}{6}=\frac{1}{2}$ , then the slope of the perpendicular line would be (-)2=-2 .

Report an Error

Example Question #1 : How To Find Out If Lines Are Perpendicular

Which of the following lines is perpendicular to the line y=3x+4

Possible Answers:

y=-3x+2

$y=\frac{1}{3}x+2$

y=3x+2

$y=-\frac{1}{3}x+2$

Correct answer:

$y=-\frac{1}{3}x+2$

Explanation:

The slope of the given line is 3. The slope of a perpendicular line is the negative inverse of the given line. In this case, that is equal to $-\frac{1}{3}$ . Therefore, the correct answer is:

$y=-\frac{1}{3}x+2$

Report an Error

Example Question #2 : How To Find Out If Lines Are Perpendicular

Given the equation of a line: $y=\frac{3}{5}x+2$

Which equation given below is perpendicular to the given line?

Possible Answers:

$y=-\frac{5}{3}x+7$

$y=-\frac{3}{5}x-2$

$y=-\frac{3}{5}x+5$

$y=-\frac{3}{2}x-4$

$y=\frac{5}{3}x+2$

Correct answer:

$y=-\frac{5}{3}x+7$

Explanation:

When looking at the equation of the given line, we know that the slope is $\frac{3}{5}$ and the y-intercept is . Any line perpendicular to the given line will create a 90 degree angle with the given line.

Now, there are INFINITE lines perpendicular to the given line, all with different y-intercepts. So in other words, the line we are looking for will have no dependence on the y-intercept, as any y-intercept will do. What we do care about is the slope of the line.

The slope of any line perpendicular to a given line has a negative reciprocal of the slope. So for this problem:

$given\;slope=\frac{3}{5}\;\rightarrow\;perpendicual\;slope=-\frac{5}{3}$

The only line that has this slope is

$y=-\frac{5}{3}x+7$

Report an Error

View Tutors

Dwarka
Certified Tutor

Birla Institute of Technology Science, Bachelors, Electronics Engg. Case Western Reserve University, Masters, Computer Engg;...

View Tutors

Joy
Certified Tutor

Boston University, Bachelor in Arts, Conservation Biology.

View Tutors

Mary Ann
Certified Tutor

Northern Illinois University, Bachelor of Science, Science Teacher Education. National Louis University, Master of Science, E...

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in Seattle, SAT Tutors in Boston, English Tutors in Los Angeles, Physics Tutors in Phoenix, Spanish Tutors in Philadelphia, Spanish Tutors in Chicago, Physics Tutors in New York City, Algebra Tutors in San Diego, Algebra Tutors in Philadelphia, English Tutors in Dallas Fort Worth

Popular Courses & Classes

ISEE Courses & Classes in Atlanta, GMAT Courses & Classes in Miami, LSAT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Chicago, SSAT Courses & Classes in Houston, GMAT Courses & Classes in Washington DC, GRE Courses & Classes in Seattle, SAT Courses & Classes in Denver, GMAT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Boston

Popular Test Prep

ACT Test Prep in Seattle, GMAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in Dallas Fort Worth, SAT Test Prep in San Diego, LSAT Test Prep in Atlanta, SAT Test Prep in Denver, GRE Test Prep in Boston, LSAT Test Prep in New York City, ISEE Test Prep in Phoenix, SAT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : Intermediate Geometry

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #1 : How To Find The Equation Of A Perpendicular Line

Example Question #4 : How To Find The Equation Of A Perpendicular Line

Example Question #7 : How To Find The Equation Of A Perpendicular Line

Example Question #1 : How To Find The Slope Of A Perpendicular Line

Example Question #1 : How To Find The Slope Of A Perpendicular Line

Example Question #1 : How To Find The Slope Of A Perpendicular Line

Example Question #11 : Perpendicular Lines

Example Question #1 : How To Find The Slope Of A Perpendicular Line

Example Question #1 : How To Find Out If Lines Are Perpendicular

Example Question #2 : How To Find Out If Lines Are Perpendicular

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: