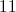Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : Intermediate Geometry

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1341 : Intermediate Geometry

A line segment begins from the origin and is 10 units long, which of the following points could NOT be an endpoint for the line segment?

Possible Answers:

(-6,8)

$(7,\sqrt{51})$

(6,8)

(5,9)

$(\sqrt{15},-\sqrt{85})$

Correct answer:

(5,9)

Explanation:

By the distance formula, the sum of the squares of each point must add up to 10 squared. The only point that doesn't fufill this requirement is (5,9)

Report an Error

Example Question #1342 : Intermediate Geometry

A line segment is drawn starting from the origin and terminating at the point (15,8) . What is the length of the line segment?

Possible Answers:

$\sqrt{264}$

$\sqrt{285}$

Correct answer:

Explanation:

Using the distance formula, $\sqrt{8^{2}+15^{2}} = 17$

Report an Error

Example Question #3 : Distance Formula

What is the distance between (-2,-3) and (6,12) ?

Possible Answers:

Correct answer:

Explanation:

In general, the distance formula is given by: $d=\sqrt{(x_{2}-x_{1})^{2}+{(y_{2}-y_{1})^{2}}}$ and is based on the Pythagorean Theorem.

Let $P_{1}=(-2,-3)$ and $P_{2}= (6,12)$

So the equation to soolve becomes $d=\sqrt{(6-(-2))^{2}+{(12-(3))^{2}}}$ or d=17

Report an Error

Example Question #3 : Distance Formula

If we graph the equation y=-2x+4 what is the distance from the y-intercept to the x-intercept?

Possible Answers:

$\sqrt{5}$

$2\sqrt{5}$

$2\sqrt{6}$

$\sqrt{6}$

Correct answer:

$2\sqrt{5}$

Explanation:

First, you must figure out where the x and y intercepts lie. To do this we begin by plugging in y=0 to our equation, giving us -2x+4=0 . Thus x=2 . So our x-intercept is the point (2,0) . We then plug in x=0 , giving us y=4 , so we know our y-intercept is the point (0,4) . We then use the distance formula $d=\sqrt{(x_{1}-x_{2})^2+(y_{1}-y_{2})^2}$ and plug in our points, giving us $d=\sqrt{(2-0)^2+(0-4)^2}=\sqrt{20}=2\sqrt{5}$

Report an Error

Example Question #4 : Distance Formula

Find the distance of the line connecting the pair of points

(0,0) and (5, 12) .

Possible Answers:

Correct answer:

Explanation:

By the distance formula

$\sqrt{(x_2-x_1)^2+(y_2-y_1)^2 }$

where (x_1,y_1)=(0,0) and (x_2,y_2)=(5,12)

we have

$\sqrt{(5-0)^2+(12-0)^2 }=\sqrt{(5)^2+(12)^2}= \sqrt{25+144} = \sqrt{169} = 13$

Report an Error

Example Question #5 : Distance Formula

Find the distance of the line connecting the pair of points

(1, 2) and (4, 6) .

Possible Answers:

Correct answer:

Explanation:

By the distance formula

$\sqrt{(x_2-x_1)^2+(y_2-y_1)^2 }$

where (x_1,y_1)=(1,2) and (x_2,y_2)=(4,6)

we have

$\sqrt{(4-1)^2+(6-2)^2 }=\sqrt{(3)^2+(4)^2}= \sqrt{9+16} = \sqrt{25} = 5$

Report an Error

Example Question #3 : How To Find The Length Of A Line With Distance Formula

Find the length of $\small y = \frac{1}{5} x - 2$ for $\small -2 \leq x \leq 5$

Possible Answers:

$\small \sqrt{36.56}$

$\small \sqrt{26.96}$

$\small \small \sqrt{60.56}$

$\small \small \sqrt{50.96}$

$\small \sqrt{9.36}$

Correct answer:

$\small \small \sqrt{50.96}$

Explanation:

To find the distance, first we have to find the specific coordinate pairs that we're finding the distance between. We know the x-values, so to find the y-values we can plug these endpoint x-values into the line:

$\small y = \frac{1}{5}(-2)-2$ first multiply

$\small y = -0.4 - 2$ then subtract

$\small y = -2.4$

$\small y = \frac{1}{5}(5)-2$ first multiply

$\small y = 1 - 2$ then subtract

$\small y = -1$

Now we know that we're finding the distance between the points $\small \small (5, -1)$ and $\small (-2, -2.4)$ . We can just plug these values into the distance formula, using the first pair as $\small (x_{1}, y_{1})$ and the second pair as $\small (x_{2}, y_{2})$ . It would work either way since we are squaring these values, this just makes it easier.

$\small \sqrt{(x_{1}-x_{2})^2 + (y_{1}- y_{2})^2}$

$\small \sqrt{(5--2)^2 + (-1 - -2.4)^2 }$

$\small \sqrt{(5+2)^2 + (-1 + 2.4)^2}$

$\small \sqrt{7^2 + 1.4^2}$

$\small \sqrt{49+1.96} = \sqrt{50.96}$

Report an Error

Example Question #3 : Distance Formula

Find the length of $\small y = -3x + 4$ for $\small 0 \leq x \leq 5$

Possible Answers:

$4\sqrt{17}$

$\small \sqrt{554}$

$5\sqrt{10}$

$\small \small \sqrt{74}$

Correct answer:

$5\sqrt{10}$

Explanation:

$\small \small y = -3(0)+4$ first multiply

$\small \small y = 0 +4$ then add

$\small \small y = 4$

$\small \small y =-3(5)+4$ first multiply

$\small \small y = -15 +4$ then add

$\small \small y = -11$

Now we know that we're finding the distance between the points $\small (0,4)$ and $\small (5, -11)$ . We can just plug these values into the distance formula, using the first pair as $\small (x_{1}, y_{1})$ and the second pair as $\small (x_{2}, y_{2})$ . Note that it would work either way since we are squaring these values anyway.

$\small \sqrt{(x_{1}-x_{2})^2 + (y_{1}- y_{2})^2}$

$\small \small \sqrt{(0-5)^2 + (4 - -11)^2 }$

$\small \small \sqrt{(-5)^2 + (15)^2}$

$\small \small \sqrt{25 + 225} = \sqrt{250}$

Report an Error

Example Question #4 : How To Find The Length Of A Line With Distance Formula

Find the length of the line $\small y= \frac{1}{2}x - 6$ for $\small -1 \leq y \leq 8$

Possible Answers:

$\small \sqrt{733}$

$9\sqrt{5}$

$\small \sqrt{481}$

$\small \sqrt{137.25}$

$\small \sqrt{373}$

Correct answer:

$9\sqrt{5}$

Explanation:

To find the distance, first we have to find the specific coordinate pairs that we're finding the distance between. We know the y-values, so to find the x-values we can plug these endpoint y-values into the line:

$\small -1 = \frac{1}{2}x - 6$ add 6 to both sides

$\small 5 = \frac{1}{2} x$ multiply by 2

10 = x this endpoint is (10, -1)

$\small 8 = \frac{1}{2} x -6$ add 6 to both sides

$\small 14 = \frac{1}{2}x$ multiply by 2

$\small 28 = x$ this endpoint is (28, 8)

Now we can plug these two endpoints into the distance formula:

$\small \sqrt{(x_{1}- x_{2})^2 + (y_{1} - y_{2})^2 }$ note that it really does not matter which pair we use as $\small (x_{1}, y_{1})$ and which as $\small (x_{2}, y_{2})$ since we'll be squaring these differences anyway, just as long as we are consistent.

$\small \sqrt{(28 - 10)^2 + (8 - - 1 )^2 }$

$\small \sqrt{18^2 + 9^2 }$

$\small \sqrt{324 + 81 } = \sqrt{405}=9\sqrt{5}$

Report an Error

Example Question #6 : Distance Formula

Find the length of $y = \frac{1}{5} x + 7$ for the interval $-5 \leq x \leq 10$ .

Possible Answers:

15.297

5.099

5.831

16.155

15.033

Correct answer:

15.297

Explanation:

To find this length, we need to know the y-coordinates for the endpoints.

First, plug in -5 for x:

$y = \frac{1}{5}(-5) + 7 = -1 + 7 = 6$

Next, plug in 10 for x:

$y = \frac{1}{5} (10 ) + 7 = 2 + 7 = 9$

So we are finding the distance between the points (-5, 6) and (10, 9 )

We will use the distance formula, $\sqrt{(x_1 - x_2)^2 + (y_1 - y_2 ) ^2 }$ . We could assign either point as (x_1, y_1) and it would still work, but let's choose (10, 9 ) :

$\sqrt{(10 - - 5 )^2 + (9 - 6 )^ 2 } = \sqrt{15^2 + 3^2 } = \sqrt{225 + 9 } = \sqrt{234} \approx 15.297$

Report an Error

View Tutors

Kinnedi
Certified Tutor

North America Montessori, Associate, Education.

View Tutors

Allison
Certified Tutor

Asbury University, Bachelor of Education, Mathematics Teacher Education.

View Tutors

Sarah
Certified Tutor

University of Houston, Bachelors, Psychology.

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Los Angeles, Physics Tutors in Washington DC, LSAT Tutors in Dallas Fort Worth, Calculus Tutors in Seattle, GRE Tutors in San Francisco-Bay Area, MCAT Tutors in Houston, Statistics Tutors in Denver, Spanish Tutors in Philadelphia, French Tutors in Chicago, Biology Tutors in Houston

Popular Courses & Classes

LSAT Courses & Classes in Miami, SSAT Courses & Classes in Washington DC, SSAT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Atlanta, ISEE Courses & Classes in New York City, LSAT Courses & Classes in Seattle, SSAT Courses & Classes in Seattle, SAT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Phoenix, ACT Courses & Classes in New York City

Popular Test Prep

GMAT Test Prep in Seattle, GRE Test Prep in Miami, ACT Test Prep in New York City, SAT Test Prep in San Francisco-Bay Area, ISEE Test Prep in Los Angeles, LSAT Test Prep in Boston, SSAT Test Prep in Dallas Fort Worth, SSAT Test Prep in Atlanta, GRE Test Prep in Phoenix, ISEE Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : Intermediate Geometry

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #1341 : Intermediate Geometry

Example Question #1342 : Intermediate Geometry

Example Question #3 : Distance Formula

Example Question #3 : Distance Formula

Example Question #4 : Distance Formula

Example Question #5 : Distance Formula

Example Question #3 : How To Find The Length Of A Line With Distance Formula

Example Question #3 : Distance Formula

Example Question #4 : How To Find The Length Of A Line With Distance Formula

Example Question #6 : Distance Formula

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: