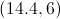Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : Intermediate Geometry

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #63 : Lines

Find the length of y = -2x + 3 for the interval $-10 \leq y \leq 15$ .

Possible Answers:

27.951

25.005

22.355

13.463

9.657

Correct answer:

27.951

Explanation:

First, we need to figure out the x-coordinates of the endpoints so that we can use the distance formula, $\sqrt{(x_1 - x_2 )^2 + (y_1 - y_2 ) ^ 2 }$

Plug in -10 for y and solve for x:

-10 = -2x + 3 subtract 3 from both sides

-13 = -2x divide both sides by -2

6.5 = x

Plug in 15 for y and solve for x:

15 = -2x + 3 subtract 3 from both sides

12 = -2x divide both sides by -2

-6 = x

The endpoints are (6.5, -10) and (-6, 15 ) . We could choose either point to be (x_1, y_1) . Let's choose (6.5, -10 ) .

$\sqrt{(6.5 -- 6 )^2 + (-10 - 15 )^2 }= \sqrt { 12.5^2 + (-25)^2 } = \sqrt{156.25 + 625}= \sqrt{781.25} \approx 27.951$

Report an Error

Example Question #11 : How To Find The Length Of A Line With Distance Formula

Find the length of the line 2x - 4 y + 10 = 0 for the interval $-5 \leq x \leq 0$ .

Possible Answers:

15.811

7.500

4.330

2.500

5.590

Correct answer:

5.590

Explanation:

To calculate the distance, first find the y-coordinates of the endpoints by plugging the x-coordinates into the equation.

First plug in -5

2(-5) - 4y + 10 = 0

-10 -4y + 10 = 0 combining like terms, we get -10 + 10 is 0

-4 y = 0 divide by -4

y = 0

Now plug in 0

2(0 ) - 4 y + 10 = 0

-4y + 10 = 0 subtract 10 from both sides

-4y = -10 divide by -4

y = 2.5

The endpoints are (-5, 0 ) and (0, 2.5) , and now we can plug these points into the distance formula:

$\sqrt{(-5 - 0 )^2 + (0 - 2.5)^2 } = \sqrt{(-5)^2 + (-2.5)^2 } = \sqrt{25 + 6.25} \approx 5.590$

Report an Error

Example Question #12 : How To Find The Length Of A Line With Distance Formula

Find the length of $y = \frac{1}{4}x + 3$ on the interval $- 8 \leq x \leq 12$ .

Possible Answers:

21.190

6.403

20.616

8.062

8.602

Correct answer:

20.616

Explanation:

To find the length, we need to first find the y-coordinates of the endpoints.

First, plug in -8 for x:

$y = \frac{1}{4} (-8) + 3 = -2 + 3 = 1$

Now plug in 12 for x:

$y = \frac{1}{4} (12 ) + 3 = 3 + 3 = 6$

Our endpoints are (-8, 1) and (12, 6 ) .

To find the length, plug these points into the distance formula:

$\sqrt{(6-1)^2 + (12--8)^2 } = \sqrt{5^2 + 20^2 } = \sqrt{25 + 400 } \approx 20.616$

Report an Error

Example Question #13 : Distance Formula

Jose is walking from his house to the grocery store. He walks 120 feet north, then turns left to walk another 50 feet west. On the way back home, Jose finds a straight line shortcut back to his house. How long is this shortcut?

Possible Answers:

$150\ ft.$

$170\ ft.$

$90\ ft.$

$130\ ft.$

Correct answer:

$130\ ft.$

Explanation:

When walking north and then taking a left west, a 90 degree angle is formed. When Jose returns home going in a straight line, this will now form the hypotenuse of a right triangle. The legs of the triangle are 120 ft and 50 ft respectively.

To solve, use the pythagorean formula.

$50^{2}+120^{2}=c^{2}$

$2500+14400=c^{2}$

$16900=c^{2}$

$\sqrt{16900}=\sqrt{c^{2}}$

130=c

130 ft is the straight line distance home.

The distance formula could also be used to solve this problem.

We will assume that home is at the point (0,0)

$Distance=\sqrt{(50-0)^{2}+(120-0)^{2}}$

Distance = 130 ft.

Report an Error

Example Question #1351 : Intermediate Geometry

A line has endpoints at (8,4) and (5,10). How long is this line?

Possible Answers:

None of these.

$3\sqrt{5}$

$\sqrt{5}$

$5\sqrt{3}$

Correct answer:

$3\sqrt{5}$

Explanation:

We find the exact length of lines using their endpoints and the distance formula.

$d=\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$

Given the endpoints,

(x_1,y_1)=(8,4)

(x_2,y_2)=(5, 10)

the distance formula becomes,

$\sqrt{(5-8)^2+(10-4)^2}=\sqrt{9+36}=\sqrt{45}=\sqrt{9\cdot 5}=\mathbf{3\sqrt{5}}$ .

Report an Error

Example Question #71 : Coordinate Geometry

Find the length of a line with endpoints at (10, 2) and (5, -6) .

Possible Answers:

$\sqrt{91}$

$\sqrt{87}$

$\sqrt{89}$

$\sqrt{85}$

Correct answer:

$\sqrt{89}$

Explanation:

Recall the distance formula for a line with two endpoints $(x_1, y_1)\text{ and }(x_2, y_2)$ :

$\text{distance}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Plug in the given points to find the length of the line:

$\text{distance}=\sqrt{(5-10)^2+(-6-2)^2}=\sqrt{89}$

Report an Error

Example Question #72 : Coordinate Geometry

A line segment on the coordinate plane has its endpoints at (3.8, -1.7) and (9.2, 5.5) .

Give the length of the segment to the nearest whole tenth.

Possible Answers:

15.2

13.5

14.8

9.0

6.6

Correct answer:

9.0

Explanation:

The distance between endpoints $(x_{1}, y_{1})$ and $(x_{2}, y_{2})$ on the coordinate plane can be calculated using the distance formula

$d = \sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$

Set $x_{1}= 3.8, y_{1} =-1.7,x_{2} =9.2, y_{2}= 5.5$ , and evaluate:

$d = \sqrt{(9.2-3.8)^{2}+[5.5 -(-1.7)]^{2}}$

$= \sqrt{5.4 ^{2}+7.2^{2}}$

$= \sqrt{29.16+51.84}$

$= \sqrt{81}$

= 9 ,

the correct length.

Report an Error

Example Question #1 : How To Find Out If A Point Is On A Line With An Equation

A line passes through both the origin and the point (12,5) . Which of the following points are NOT on the line?

Possible Answers:

(20.4,8.5)

(15.6,8)

(-3,-1.25)

(6,2.5)

(14.4,6)

Correct answer:

(15.6,8)

Explanation:

Because the line passes through the origin, all of the points on the line will have an x:y ratio of 12:5 . Only $\left ( 15.6,8 \right )$ does not meet this requirement.

Report an Error

Example Question #71 : Lines

Which of the following points does NOT lie on the graph of y=x^2-3x+7

Possible Answers:

(2,5)

(5,17)

(4,12)

(1,5)

(3,7)

Correct answer:

(4,12)

Explanation:

To find if a point lies on a graph or not, simply plug the x and y values into your equation and see if it holds true. Plugging our x values into the equation y=x^2-3x+7 gives us the following:

x=1: y=(1)^2-3(1)+7=5

x=2: y=(2)^2-3(2)+7=5

x=3: y=(3)^2-3(3)+7=7

x=4: y=(4)^2-3(4)+7=11 and

x=5: y=(5)^2-3(5)+7=17

So our points are (1,5), (2,5), (3,7), (4,11), and (5,17) . This makes (4,12) the only point that does not lie on our graph.

Report an Error

Example Question #1 : How To Find Out If A Point Is On A Line With An Equation

Which of the following points exists on the line 2x-2y=1 ?

Possible Answers:

$( 1,\frac{1}{2})$

$(0,\frac{1}{2})$

(0,1)

$( 1,-\frac{1}{2})$

(1,0)

Correct answer:

$( 1,\frac{1}{2})$

Explanation:

Substitute each answer choice into the equation in question, 2x-2y=1 , in order to test if the equation is valid at the given point

Only $( 1,\frac{1}{2})$ will satisfy the equation on both the left and right side.

Report an Error

View Tutors

Monse
Certified Tutor

California intercontinental University, Master's/Graduate, MBA with a specialization in international management and marketing.

View Tutors

Bagher
Certified Tutor

San Jose State University, Master's/Graduate, Physics.

View Tutors

Shakeel
Certified Tutor

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GMAT Tutors in Chicago, Math Tutors in San Diego, ISEE Tutors in Los Angeles, Physics Tutors in Denver, Chemistry Tutors in Philadelphia, Calculus Tutors in Phoenix, SAT Tutors in Dallas Fort Worth, Statistics Tutors in Houston, Biology Tutors in Houston, GMAT Tutors in Dallas Fort Worth

Popular Courses & Classes

ISEE Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Denver, ISEE Courses & Classes in San Diego, GMAT Courses & Classes in Seattle, SAT Courses & Classes in Seattle, GMAT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Seattle, LSAT Courses & Classes in Chicago, GMAT Courses & Classes in New York City, Spanish Courses & Classes in Philadelphia

Popular Test Prep

MCAT Test Prep in Seattle, MCAT Test Prep in Dallas Fort Worth, LSAT Test Prep in New York City, SAT Test Prep in Atlanta, ISEE Test Prep in Boston, LSAT Test Prep in Philadelphia, SAT Test Prep in Seattle, GMAT Test Prep in New York City, SAT Test Prep in Philadelphia, ACT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : Intermediate Geometry

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #63 : Lines

Example Question #11 : How To Find The Length Of A Line With Distance Formula

Example Question #12 : How To Find The Length Of A Line With Distance Formula

Example Question #13 : Distance Formula

Example Question #1351 : Intermediate Geometry

Example Question #71 : Coordinate Geometry

Example Question #72 : Coordinate Geometry

Example Question #1 : How To Find Out If A Point Is On A Line With An Equation

Example Question #71 : Lines

Example Question #1 : How To Find Out If A Point Is On A Line With An Equation

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: