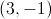We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : Intermediate Geometry

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : How To Find The Radius Of A Sphere

If the volume of a sphere is $1\:unit$ , what is the sphere's exact radius?

Possible Answers:

$\sqrt{\frac{1}{\pi}}\:units$

$\sqrt{\frac{2}{3\pi}}\:units$

$\sqrt[3]{\frac{4\pi}{3}}\:units$

$\sqrt{\pi}\:units$

$\sqrt[3]{\frac{3}{4\pi}}\:units$

Correct answer:

$\sqrt[3]{\frac{3}{4\pi}}\:units$

Explanation:

Write the formula for the volume of a sphere:

$V=\frac{4}{3}\pi r^3$

Plug in the given volume and solve for the radius, .

$1=\frac{4}{3}\pi r^3$

Start by multiplying each side of the equation by $\frac{3}{4}$ :

$\frac{3}{4}\cdot1=\frac{4}{3}\pi r^3\cdot\frac{3}{4}$

$\frac{3}{4}=\pi r^3$

Now, divide each side of the equation by $\pi$ :

$\frac{3}{4}\div\pi=\pi r^3\div\pi$

$\frac{3}{4\pi}=r^3$

Finally, take the cubed root of each side of the equation:

$r=\sqrt[3]{\frac{3}{4\pi}}$

Report an Error

Example Question #5 : How To Find The Radius Of A Sphere

Given the volume of a sphere is $\frac{4}{3}\pi\:cm^3$ , what is the radius?

Possible Answers:

$\frac{\sqrt2}{3}\:cm$

$\frac{4}{3}\:cm$

$1\:cm$

$\frac{1}{2}\:cm$

$\frac{1}{4}\:cm$

Correct answer:

$1\:cm$

Explanation:

The equation for the volume of a sphere is:

$V=\frac{4}{3}\pi r^3$ , where is the length of the sphere's radius.

Plug in the given volume and solve for to calculate the sphere's radius:

$\frac{4}{3}\pi=\frac{4}{3}\pi r^3$

1=r^3

r=1

Report an Error

Example Question #2 : How To Find The Radius Of A Sphere

If the volume of a sphere is $4\:m^3$ , what is the radius of the sphere?

Possible Answers:

$\sqrt[3]{\frac{3}{\pi}}\:m$

$\sqrt[3]{\frac{1}{3\pi}}\:m$

$\sqrt[3]{\frac{16}{3\pi}}\:m$

$\sqrt[3]{3\pi}\:m$

$\sqrt[3]{\frac{3}{\pi}}\:m$

Correct answer:

$\sqrt[3]{\frac{3}{\pi}}\:m$

Explanation:

The formula for the volume of a sphere is:

$V=\frac{4}{3}\pi r^3$ , where is the sphere's radius.

Plug in the volume and solve for , the sphere's radius:

$4=\frac{4}{3}\pi r^3$

$3=\pi r^3$

$\frac{3}{\pi}=r^3$

$r=\sqrt[3]{\frac{3}{\pi}}\:m$

Report an Error

Example Question #3 : How To Find The Radius Of A Sphere

Find the radius of a sphere if the surface area is $8\pi\:cm^2$ .

Possible Answers:

$2\:cm$

$\sqrt{2}\:cm$

$\sqrt{\frac{1}{2}}\:cm$

$\frac{1}{2}\:cm$

$2\sqrt 2\:cm$

Correct answer:

$\sqrt{2}\:cm$

Explanation:

The formula for the surface area of a sphere is:

$SA=4\pi r^2$

Substitute the given value for the sphere's surface area into the equation and solve for to find the radius:

$8\pi=4\pi r^2$

2=r^2

$r=\sqrt2\:cm$

Report an Error

Example Question #1 : How To Find The Radius Of A Sphere

Find the radius of a sphere if its surface area is $8\:in^2$ .

Possible Answers:

$\sqrt\frac{\pi}{2}\:in$

$\sqrt\frac{2}{\pi}\:in$

$\sqrt\frac{\pi}{8}\:in$

$\sqrt\frac{8}{\pi}\:in$

$\sqrt2\:in$

Correct answer:

$\sqrt\frac{2}{\pi}\:in$

Explanation:

The surface area formula for a sphere is:

$A=4\pi r^2$ , where is the sphere's radius.

Substitute the given value for the sphere's area into the equation and solve for to find the radius:

$8=4\pi r^2$

$\frac{2}{\pi}= r^2$

$r=\sqrt{\frac{2}{\pi}}\:in$

Report an Error

Example Question #1 : Midpoint Formula

What is the midpoint between (-1,3) and (7,-5) ?

Possible Answers:

(4,-4)

(4,-1)

(3,0)

(2,2)

(3,-1)

Correct answer:

(3,-1)

Explanation:

The midpoint is given by taking the mean, or average, of the and coordinates separately.

Let $P_{1}=\left ( 7,5 \right )$ and $P_{2} = \left (-1,3 \right )$

So the midpoint formula becomes $\frac{x_{1}\ +\ x_{2}}{2}= \frac{7-1}{2}=3$ and $\frac{y_{1}+y_{2}}{2}= \frac{-5 +3}{2}=-1$

So the midpoint is (3,-1)

Report an Error

Example Question #1 : Midpoint Formula

What is the midpoint of a line segment connecting the points $\left ( -5,6 \right )$ and $\left ( -3,2 \right )\ ?$

Possible Answers:

$\left ( -1,2 \right )$

$\left ( -4,2 \right )$

$\left ( -1,4 \right )$

$\left ( -4,4 \right )$

Correct answer:

$\left ( -4,4 \right )$

Explanation:

Use the midpoint formula:

$(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})=midpoint$

$(\frac{-5+(-3)}{2}, \frac{6+2}{2})=(\frac{-8}{2}, \frac{8}{2})=(-4,4)$

Report an Error

Example Question #2 : Midpoint Formula

Given two points $\left ( -3,-3 \right )$ and $\left ( -1,1 \right )$ and a line segment that connects the two.

What is the midpoint of the line segment? Addtionally, what is the length of the line segment?

Possible Answers:

Midpoint: $\left ( -1,-1 \right )$

Length: $4\sqrt3$

Midpoint: $\left ( -2,-1 \right )$

Length: $2\sqrt{5}$

Midpoint: $\left ( -1,-2 \right )$

Length: $2\sqrt5$

Midpoint: $\left ( -1,-2 \right )$

Length:

Midpoint: $\left ( -2,-1 \right )$

Length: $\sqrt5$

Correct answer:

Midpoint: $\left ( -2,-1 \right )$

Length: $2\sqrt{5}$

Explanation:

The midpoint formula is as follows:

$midpoint = (\frac{x_1 +x_2}{2},\frac{y_1+y_2}{2})$

This makes sense; it is as simple as the average of the and components of each point.

For this problem, $x_1=-3,x_2=-1,y_1=-3,and\: y_2=1$ .

So the midpoint is $\left ( -2,-1 \right )$

The distance formula is as follows:

$distance=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

The order you put the first and second components of each point does NOT matter, when a positive or negative number is squared, it will always come out positive.

$(2)^2=4\; and\; (-4)^2=16$

So the distance is $\sqrt{(-3+1)^2+(-3-1)^2} =\sqrt{4+16}=\sqrt{20}=2\sqrt{5}$

Report an Error

Example Question #3 : How To Find The Midpoint Of A Line Segment

Find the midpoint of a line segment going from (-2,-9) to (-6,-1) .

Possible Answers:

(-1,3)

(-4,4)

(2,4)

(3,5)

(-4,-5)

Correct answer:

(-4,-5)

Explanation:

To find the midpoint of a line segment, you must find the mean of the x values and the mean of the y values.

Our x values are and to find their mean, we do (-2+-6)/2=-4 .

Our y values are and , so our mean is (-9+-1)/2=-5 . Therefore, our midpoint must be (-4,-5) .

Report an Error

Example Question #2 : Coordinate Geometry

Find the coordinate of the midpoint of the line segment connecting the pair of points

(2, 2) and (4, 12) .

Possible Answers:

(3, 7)

Cannot be determined

(2, 7)

(1, 5)

Correct answer:

(3, 7)

Explanation:

The coordinate of the midpoint of the line segment connecting a pair of points is

$\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)$

So for the pair of points (x_1,y_1)=(2,2) and (x_2,y_2)=(4,12) ,

we get:

$\left(\frac{2+4}{2}, \frac{2+12}{2}\right)=(3, 7)$

Report an Error

View Tutors

Justin
Certified Tutor

Vanderbilt University, Bachelor, Computer Science, Mathematics, & Philosophy.

View Tutors

Ria
Certified Tutor

University of British Columbia, Bachelor in Arts, Psychology.

View Tutors

John
Certified Tutor

Arizona State University, Bachelor of Science, Microbiology.

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Philadelphia, Calculus Tutors in Los Angeles, GRE Tutors in Denver, Math Tutors in Boston, Algebra Tutors in Philadelphia, Spanish Tutors in Phoenix, Reading Tutors in Chicago, GMAT Tutors in Miami, Spanish Tutors in Seattle, Chemistry Tutors in Denver

Popular Courses & Classes

ACT Courses & Classes in Chicago, ISEE Courses & Classes in San Diego, Spanish Courses & Classes in Phoenix, MCAT Courses & Classes in Denver, LSAT Courses & Classes in San Diego, GMAT Courses & Classes in Seattle, GMAT Courses & Classes in Denver, LSAT Courses & Classes in New York City, ISEE Courses & Classes in Boston, GMAT Courses & Classes in Atlanta

Popular Test Prep

MCAT Test Prep in Dallas Fort Worth, GRE Test Prep in Miami, GMAT Test Prep in Philadelphia, GMAT Test Prep in Atlanta, ACT Test Prep in Boston, GMAT Test Prep in Dallas Fort Worth, GRE Test Prep in Boston, SSAT Test Prep in Phoenix, MCAT Test Prep in San Francisco-Bay Area, ISEE Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : Intermediate Geometry

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #2 : How To Find The Radius Of A Sphere

Example Question #5 : How To Find The Radius Of A Sphere

Example Question #2 : How To Find The Radius Of A Sphere

Example Question #3 : How To Find The Radius Of A Sphere

Example Question #1 : How To Find The Radius Of A Sphere

Example Question #1 : Midpoint Formula

Example Question #1 : Midpoint Formula

Example Question #2 : Midpoint Formula

Example Question #3 : How To Find The Midpoint Of A Line Segment

Example Question #2 : Coordinate Geometry

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: