All HSPT Math Resources
Example Questions
Example Question #2 : Know And Use The Formulas For The Volumes Of Cones, Cylinders, And Spheres: Ccss.Math.Content.8.G.C.9
The height of a cylinder is 3 inches and the radius of the circular end of the cylinder is 3 inches. Give the volume and surface area of the cylinder.
The volume of a cylinder is found by multiplying the area of one end of the cylinder (base) by its height or:
where 

The surface area of the cylinder is given by:
where 


Example Question #141 : Geometry
The end (base) of a cylinder has an area of 
The area of the end (base) of a cylinder is 
The height of the cylinder is half of the radius of the base of the cylinder, that means:
The volume of a cylinder is found by multiplying the area of one end of the cylinder (base) by its height:
or
Example Question #4 : Know And Use The Formulas For The Volumes Of Cones, Cylinders, And Spheres: Ccss.Math.Content.8.G.C.9
We have two right cylinders. The radius of the base Cylinder 1 is 
The volume of a cylinder is:
where 


So we can write:
and
Now we can summarize the given information:
Now substitute them in the 
Example Question #731 : Geometry
Two right cylinders have the same height. The radius of the base of the first cylinder is two times more than that of the second cylinder. Compare the volume of the two cylinders.
The volume of a cylinder is:
where 

We know that
and

So we can write:
Example Question #491 : Grade 8
A car dealership wants to fill a large spherical advertising ballon with helium. It can afford to buy 1,000 cubic yards of helium to fill this balloon. What is the greatest possible diameter of that balloon (nearest tenth of a yard)?
The volume of a sphere, given its radius, is
Set 

The diameter is twice this, or 12.4 yards.
Example Question #492 : Grade 8
The diameter of a sphere is 

The diameter of a sphere is 
The volume enclosed by a sphere is given by the formula:

Example Question #493 : Grade 8
A spherical balloon has a diameter of 10 meters. Give the volume of the balloon.
The volume enclosed by a sphere is given by the formula:
where 

Example Question #151 : Geometry
The volume of a sphere is 1000 cubic inches. What is the diameter of the sphere.
The volume of a sphere is:
Where 


So we can get:
Example Question #91 : Geometry

Give the volume of the above box in cubic centimeters.
100 centimeters make one meter, so convert each of the dimensions of the box by multiplying by 100.


Use the volume formula, substituting 

Example Question #1331 : Concepts
A cube made of nickel has sidelength 20 centimeters, Nickel has a density of 8.9 grams per cubic centimeter. What is the mass of this cube?
The volume of the cube is 


Certified Tutor
Certified Tutor
All HSPT Math Resources

































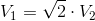


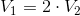














![r \approx \sqrt[3]{238.7} \approx 6.2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/92097/gif.latex)
































