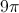Call Now to Set Up Tutoring:

(888) 888-0446

HSPT Math : Concepts

Study concepts, example questions & explanations for HSPT Math

Create An Account

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #11 : How To Find The Volume Of A Cylinder

What is the volume of a cylinder with a radius of 4 and a height of 5?

Possible Answers:

$80\pi$

$40\pi$

$60\pi$

$72\pi$

$54\pi$

Correct answer:

$80\pi$

Explanation:

$volume = \pi r^{2}h = \pi \cdot 4^{2} \cdot 5 = 80\pi$

Report an Error

Example Question #12 : How To Find The Volume Of A Cylinder

Claire's cylindrical water bottle is 9 inches tall and has a diameter of 6 inches. How many cubic inches of water will her bottle hold?

Possible Answers:

$81\pi$

$45\pi$

$54\pi$

$18\pi$

$324\pi$

Correct answer:

$81\pi$

Explanation:

The volume is the area of the base times the height. The area of the base is $\pi r^{2}$ , and the radius here is 3. $\pi\cdot 3^{2}\cdot 9=81\pi$

Report an Error

Example Question #13 : Cylinders

What is the volume of a circular cylinder whose height is 8 cm and has a diameter of 4 cm?

Possible Answers:

$12\pi \ cm^{3}$

$64\pi \ cm^{3}$

$128\pi \ cm^{3}$

$32\pi \ cm^{3}$

$16\pi \ cm^{3}$

Correct answer:

$32\pi \ cm^{3}$

Explanation:

The volume of a circular cylinder is given by $V = \pi r^{2}h$ where is the radius and is the height. The diameter is given as 4 cm, so the radius would be 2 cm as the diameter is twice the radius.

Report an Error

Example Question #832 : Geometry

You have tall glass with a radius of 3 inches and height of 6 inches. You have an ice cube tray that makes perfect cubic ice cubes that have 0.5 inch sides. You put three ice cubes in your glass. How much volume do you have left for soda? The conversion factor is $1\hspace{1 mm}inch^3=0.0163871\hspace{1 mm}L$ .

Possible Answers:

$54\pi\hspace{1 mm}inches^3$

$\frac{3}{8}inches^3$

$2.77\hspace{1 mm}L$

$1.69\hspace{1 mm}L$

$169.27\hspace{1 mm}mL$

Correct answer:

$2.77\hspace{1 mm}L$

Explanation:

First we will calculate the volume of the glass. The volume of a cylinder is

$V=\pi r^2 h$

$V=\pi (3\hspace{1 mm}inches)^2 \times 6\hspace{1 mm}inches = 54\pi\hspace{1 mm}inches^3$

Now we will calculate the volume of one ice cube:

$V=lwh=l^3=(\frac{1}{2}\hspace{1 mm}inch)^3=\frac{1}{8}\hspace{1 mm}inches^3$

The volume of three ice cubes is $\frac{3}{8}\hspace{1 mm}inches^3$ . We will then subtract the volume taken up by ice from the total volume:

$54\pi\hspace{1 mm}inches^3-\frac{1}{8}\hspace{1 mm}inches^3\approx 169.27\hspace{1 mm}inches^3$

Now we will use our conversion factor:

$169.27\hspace{1 mm}inches^3\times \frac{0.016387\hspace{1 mm}L}{1\hspace{1 mm}inch^3}=2.77\hspace{1 mm}L$

Report an Error

Example Question #1 : Cylinders

A water glass has the shape of a right cylinder. The glass has an interior radius of 2 inches, and a height of 6 inches. The glass is 75% full. What is the volume of the water in the glass (in cubic inches)?

Possible Answers:

$9 \pi$

$36 \pi$

$12 \pi$

$18 \pi$

$24 \pi$

Correct answer:

$18 \pi$

Explanation:

The volume of a right cylinder with radius r=2 and height h=6 is:

$\pi r^2 h = \pi (2)^2 (6) = 24 \pi$

Since the glass is only 75% full, only 75% of the interior volume of the glass is occupied by water. Therefore the volume of the water is:

$24 \pi \times ( 75 / 100 ) = 24 \pi (0.75) = 18 \pi$

Report an Error

Example Question #14 : Cylinders

A circle has a circumference of $4\pi$ and it is used as the base of a cylinder. The cylinder has a surface area of $16\pi$ . Find the volume of the cylinder.

Possible Answers:

$6\pi$

$8\pi$

$4\pi$

$2\pi$

$10\pi$

Correct answer:

$8\pi$

Explanation:

Using the circumference, we can find the radius of the circle. The equation for the circumference is $2\pi r$ ; therefore, the radius is 2.

Now we can find the area of the circle using $\pi r^{2}$ . The area is $4\pi$ .

Finally, the surface area consists of the area of two circles and the area of the mid-section of the cylinder: $2\cdot 4\pi +4\pi h=16\pi$ , where $h$ is the height of the cylinder.

Thus, $h=2$ and the volume of the cylinder is $4\pi h=4\pi \cdot 2=8\pi$ .

Report an Error

Example Question #13 : How To Find The Volume Of A Cylinder

A metal cylindrical brick has a height of $6\ in$ . The area of the top is $25\pi\ in^2$ . A circular hole with a radius of $2\ in$ is centered and drilled half-way down the brick. What is the volume of the resulting shape?

Possible Answers:

$125\pi\ in^3$

$138\pi\ in^3$

$150\pi\ in^3$

$100\pi\ in^3$

$175\pi\ in^3$

Correct answer:

$138\pi\ in^3$

Explanation:

To find the final volume, we will need to subtract the volume of the hole from the total initial volume of the cylinder.

The volume of a cylinder is given by the product of the base area times the height: $V=A_{base}h$ .

Find the initial volume using the given base area and height.

$V_i=(25\pi)(6)=150\pi\ in^3$

Next, find the volume of the hole that was drilled. The base area of this cylinder can be calculated from the radius of the hole. Remember that the height of the hole is only half the height of the block.

$V_{hole}=(\pi r^2)h$

$V_{hole}=(\pi(2)^2)(3)=(4\pi)(3)=12\pi\ in^3$

Finally, subtract the volume of the hole from the total initial volume.

$150\pi-12\pi=138\pi\ in^3$

Report an Error

Example Question #14 : How To Find The Volume Of A Cylinder

What is the volume of a cylinder with a diameter of 13 inches and a height of 27.5 inches?

Possible Answers:

$381.44\pi \ in^{3}$

$357.5\pi \ in^{3}$

$2583.1\pi \ in^{3}$

$4647.5\ in^{3}$

$1161.88\pi \ in^{3}$

Correct answer:

$1161.88\pi \ in^{3}$

Explanation:

The equation for the volume of a cylinder is V = Ah, where A is the area of the base and h is the height.

Thus, the volume can also be expressed as V = πr²h.

The diameter is 13 inches, so the radius is 13/2 = 6.5 inches.

Now we can easily calculate the volume:

V = 6.5²π * 27.5 = 1161.88π in³

Report an Error

Example Question #21 : Cylinders

Two cylinders are full of milk. The first cylinder is 9” tall and has a base diameter of 3”. The second cylinder is 9” tall and has a base diameter of 4”. If you are going to pour both cylinders of milk into a single cylinder with a base diameter of 6”, how tall must that cylinder be for the milk to fill it to the top?

Possible Answers:

12"

6.25"

30"

Correct answer:

6.25"

Explanation:

Volume of cylinder = π * (base radius)² x height = π * (base diameter / 2 )² x height

Volume Cylinder 1 = π * (3 / 2 )² x 9 = π * (1.5 )² x 9 = π * 20.25

Volume Cylinder 2 = π * (4 / 2 )² x 9 = π * (2 )² x 9 = π * 36

Total Volume = π * 20.25 + π * 36

Volume of Cylinder 3 = π * (6 / 2 )² x H = π * (3 )² x H = π * 9 x H

Set Total Volume equal to the Volume of Cylinder 3 and solve for H

π * 20.25 + π * 36 = π * 9 x H

20.25 + 36 = 9 x H

H = (20.25 + 36) / 9 = 6.25”

Report an Error

Example Question #1 : How To Find The Volume Of A Cube

A cubic box has sides of length x. Another cubic box has sides of length 4x. How many of the boxes with length x could fit in one of the larger boxes with side length 4x?

Possible Answers:

Correct answer:

Explanation:

The volume of a cubic box is given by (side length)³. Thus, the volume of the larger box is (4x)³ = 64x³, while the volume of the smaller box is x³. Divide the volume of the larger box by that of the smaller box, (64x³)/(x³) = 64.

Report an Error

View Tutors

Ana Maria
Certified Tutor

Florida International University, Bachelor of Science, Mathematics Teacher Education.

View Tutors

Usman
Certified Tutor

New York University, Bachelor in Arts, Political Science and Government.

View Tutors

Bagher
Certified Tutor

San Jose State University, Master's/Graduate, Physics.

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

LSAT Tutors in Atlanta, Biology Tutors in San Diego, Biology Tutors in Los Angeles, Calculus Tutors in Phoenix, ISEE Tutors in San Diego, English Tutors in New York City, Reading Tutors in Miami, LSAT Tutors in Los Angeles, Calculus Tutors in Philadelphia, Reading Tutors in Houston

Popular Courses & Classes

SAT Courses & Classes in Phoenix, GMAT Courses & Classes in Miami, GRE Courses & Classes in San Diego, SAT Courses & Classes in Washington DC, SAT Courses & Classes in San Diego, Spanish Courses & Classes in Washington DC, Spanish Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in San Diego, SSAT Courses & Classes in Seattle, SSAT Courses & Classes in Phoenix

Popular Test Prep

SAT Test Prep in Atlanta, GRE Test Prep in Los Angeles, SSAT Test Prep in San Diego, SAT Test Prep in Dallas Fort Worth, SSAT Test Prep in Seattle, ISEE Test Prep in San Francisco-Bay Area, SAT Test Prep in Los Angeles, ACT Test Prep in Seattle, SSAT Test Prep in Houston, GRE Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

HSPT Math : Concepts

Study concepts, example questions & explanations for HSPT Math

All HSPT Math Resources

Example Questions

Example Question #11 : How To Find The Volume Of A Cylinder

Example Question #12 : How To Find The Volume Of A Cylinder

Example Question #13 : Cylinders

Example Question #832 : Geometry

Example Question #1 : Cylinders

Example Question #14 : Cylinders

Example Question #13 : How To Find The Volume Of A Cylinder

Example Question #14 : How To Find The Volume Of A Cylinder

Example Question #21 : Cylinders

Example Question #1 : How To Find The Volume Of A Cube

All HSPT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: