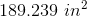Based on our prompt, we can say that the prism has dimensions that can be represented as:

Dim1: x

Dim2: 2 * Dim1 = 2x

Dim3: 2 * Dim2 = 2 * 2x = 4x

More directly stated, therefore, our dimensions are: x, 2x, and 4x. Therefore, the volume is x * 2x * 4x = 216, which simplifies to 8x³ = 216 or x³ = 27. Solving for x, we find x = 3. Therefore, our dimensions are:

x = 3

2x = 6

4x = 12

Or: 3 x 6 x 12

Now, to find the surface area, we must consider that this means that our prism has sides of the following dimensions: 3 x 6, 6 x 12, and 3 x 12. Since each side has a "matching" side opposite it, we know that we have the following values for the areas of the faces:

2 * 3 * 6 = 36

2 * 6 * 12 = 144

2 * 3 * 12 = 72

The total surface area therefore equals: 36 + 144 + 72 = 252 square units.

Converting squared units is not difficult, though you have to be careful not to make a simple mistake. It is tempting to think you can merely divide the initial value (30,096) by 12, as though you were converting from inches to feet.

Begin by thinking this through as follows. In the case of a single dimension, we know that:

1 ft = 12 in   or   1 in = (1/12) ft

Now, think the case of a square with dimensions 1 ft x 1 ft. This square has the following dimensions in inches: 12 in x 12 in. The area is therefore 12 * 12 = 144 in². This holds for all two-dimensional conversions. Therefore, the two dimensional conversion equation is:

1 ft² = 144 in²   or   1 in² = (1/144) ft²

Based on this, we can convert our value 30,096 in² thus: 30,096/144 = 209 ft².

Converting squared units is not difficult, though you have to be careful not to make a simple mistake. It is tempting to think you can merely multiply the initial value (24) by 36, as though you were converting from yards to inches.

Begin by thinking this through as follows. In the case of a single dimension, we know that:

1 yd = 36 in

Now, think the case of a square with dimensions 1 yd x 1 yd. This square has the following dimensions in inches: 36 in x 36 in. The area is therefore 36 * 36 = 1296 in². This holds for all two-dimensional conversions. Therefore, the two dimensional conversion equation is:

1 yd² = 1296 in²

Based on this, we can convert our value 24 yd² thus: 24 * 1296 = 31,104 in².

The surface area of the prism can be broken into three rectangular sides and two equilateral triangular bases.

The area of the sides is given by:  , so for all three sides we get .

The equilateral triangle is also an equiangular triangle by definition, so the base has congruent sides of 6 in and three angles of 60 degrees.  We use a special right traingle to figure out the height of the triangle: 30 - 60 - 90.  The height is the side opposite the 60 degree angle, so it becomes or 5.196. 

The area for a triangle is given by  and since we need two of them we get .

Therefore the total surface area is .

The surface area of the sphere before it was cut is equal to the following:

surface area of solid sphere = 4πr², where r is the length of the radius.

Each hemisphere will have the following shape:

In order to determine the surface area of the hemisphere, we must find the surface area of the flat region and the curved region. The flat region will have a surface area equal to the area of a circle with radius r.

area of flat part of hemisphere = πr²

The surface area of the curved portion of the hemisphere will equal one-half of the surface area of the uncut sphere, which we established to be 4πr².

area of curved part of hemisphere = (1/2)4πr² = 2πr²

The total surface area of the hemisphere will be equal to the sum of the surface areas of the flat part and curved part of the hemisphere.

total surface area of hemisphere = πr² + 2πr² = 3πr²

Finally, we must find the ratio of the surface area of the hemisphere to the surface area of the uncut sphere.

ratio = (3πr²)/(4πr²) = 3/4

The answer is 3/4.

To solve this, we must first begin by finding the radius of the sphere. To do this, recall that the volume of a sphere is:

V = (4/3)πr³

For our data, we can say:

2304π = (4/3)πr³; 2304 = (4/3)r³; 6912 = 4r³; 1728 = r³; 12 * 12 * 12 = r³; r = 12

Now, based on this, we can ascertain the surface area using the equation:

A = 4πr²

For our data, this is:

A = 4π*12² = 576π

To find the surface area, we must first find the radius.  Based on our description, this passes from (0,0) to (6,8).  This can be found using the distance formula:

6² + 8² = r²; r² = 36 + 64; r² = 100; r = 10

It should be noted that you could have quickly figured this out by seeing that (6,8) is the hypotenuse of a 6-8-10 triangle (which is a multiple of the "easy" 3-4-5).

The rest is easy.  The surface area of the sphere is defined by:

A = 4πr² = 4 * 100 * π = 400π

To begin, we must determine the dimensions of the cube. To do this, recall that the surface area of a cube is made up of six squares and is thus defined as: A = 6s², where s is one of the sides of the cube. For our data, this gives us:

726 = 6s²; 121 = s²; s = 11

Now, if the sphere is contained within the cube, that means that 11 represents the diameter of the sphere. Therefore, the radius of the sphere is 5.5 units. The surface area of a sphere is defined as: A = 4πr². For our data, that would be:

A = 4π * 5.5² = 30.25 * 4 * π = 121π

The surface area of a sphere is 4πr². The area of a circle is πr². 16/16 is equal to 1.

Let's call the radius of the sphere r. The formula for the surface area of a sphere (A) is given below:

A = 4πr²

Because the sphere is inscribed inside the cube, the diameter of the sphere is equal to the side length of the cube. Because the diameter is twice the length of the radius, the diameter of the sphere is 2r. This means that the side length of the cube is also 2r. 

The surface area for a cube is given by the following formula, where s represents the length of each side of the cube:

surface area of cube = 6s²

The formula for surface area of a cube comes from the fact that each face of the cube has an area of s², and there are 6 faces total on a cube. 

Since we already determined that the side length of the cube is the same as 2r, we can replace s with 2r.

surface area of cube = 6(2r)² = 6(2r)(2r) = 24r².

We are asked to find the ratio of the surface area of the cube to the surface area of the sphere. This means we must divide the surface area of the cube by the surface area of the sphere.

ratio = (24r²)/(4πr²)

The r² term cancels in the numerator and denominator. Also, 24/4 simplifes to 6.

ratio = (24r²)/(4πr²) = 6/π

The answer is 6/π.