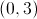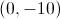Moving four units to the right increases the -coordinate by 4; moving six units up increases the -coordinate by 6. The current location is

, or .

The -coordinate changes by  units; therefore, you must move ten units in a positive horizontal direction - right.

The -coordinate changes by  units; therefore, you must move two units in a negative vertical direction - down. 

The correct response is to move right ten units and down two units.

Apply the distance formula, substituting the -coordinates for  and  and the -coordinates for  and :

A line perpendicular to a line with slope has as its slope the opposite of the reciprocal of ; this number is . The line passes through the origin, which is the point ; this is also the -intercept. In slope-intercept form, its equation can be found by substituting in the equation:

This can be rewritten in standard form as follows:

The origin is . In the following slope formula, set

,

and solve for :

 and  are represented by a horizontal line and a vertical line, respectively; therefore, their graphs are perpendicular.

As for the third equation, , this is represented by a line with slope , as seen below:

The equation is in slope-intercept form, and the slope of the line is the coefficient of , which is . It is perpendicular to a line with slope ; however, the horizontal line has slope 0, and the vertical line has undefined slope. 

The correct choice is therefore I and II.

Since you move right  units in the second step and right  units in the fourth, you will move a total of  units right; this means the -coordinate will be , which is equal to 72.

Since you move up  units in the first step and down  units in the third, you will move a total of  units up; this means the -coordinate will be , which is equal to 46.

We can form a system of equations and solve by adding, as follows:

The -intercept of the graph 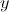of a function is the point at which it intersects the -axis - that is, at which . This point is , so evaluate :

The -intercept is .

The lateral area (not including its bases) is equal to the circumference of the base times the height of the cylinder. Think of it like a label that is wrapped around a soup can. Therefore, we can write this area as:

A = h * π * d or A = h * π * 2r = 2πrh

Now, substituting in our values, we get:

512.5π = 2 * 41*rπ; 512.5π = 82rπ

Solve for r by dividing both sides by 82π:

6.25 = r

From here, we can calculate the area of a base:

A = 6.25²π = 39.0625π

NOTE: The question asks for the area of the bases. Therefore, the answer is 2 * 39.0625π or 78.125π in².

We need to find expressions for the surface area and the volume of a cylinder. The surface area of the cylinder consists of the sum of the surface areas of the two bases plus the lateral surface area.

surface area of cylinder = surface area of bases + lateral surface area

The bases of the cylinder will be two circles with radius r. Thus, the area of each will be πr², and their combined surface area will be 2πr².

The lateral surface area of the cylinder is equal to the circumference of the circular base multiplied by the height. The circumferece of a circle is 2πr, and the height is h, so the lateral area is 2πrh.

surface area of cylinder = 2πr² + 2πrh

Next, we need to find an expression for the volume. The volume of a cylinder is equal to the product of the height and the area of one of the bases. The area of the base is πr², and the height is h, so the volume of the cylinder is πr²h.

volume = πr²h

Then, we must set the volume and surface area expressions equal to one another and solve for r in terms of h.

2πr² + 2πrh = πr²h

First, let's factor out 2πr from the left side.

2πr(r + h) = πr²h

We can divide both sides by π.

2r(r + h) = r²h

We can also divide both sides by r, because the radius cannot equal zero.

2(r + h) = rh

Let's now distribute the 2 on the left side.

2r + 2h = rh

Subtract 2r from both sides to get all the r's on one side.

2h = rh – 2r

rh – 2r = 2h 

Factor out an r from the left side.

r(h – 2) = 2h

Divide both sides by h – 2

r = 2h/(h – 2)

The answer is r = 2h/(h – 2).