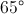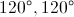Call Now to Set Up Tutoring:

(888) 888-0446

HSPT Math : Geometry

Study concepts, example questions & explanations for HSPT Math

Create An Account

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #221 : Geometry

A sphere has diameter 12. What is 75% of its volume?

Possible Answers:

$108 \pi$

$432 \pi$

$216 \pi$

$1,728 \pi$

Correct answer:

$216 \pi$

Explanation:

The radius of a sphere is half its diameter, which here is 12, so the radius is 6. The volume of the sphere can be calculated by setting r = 6 in the formula:

$V = \frac{4}{3} \pi r ^{3}$

$V = \frac{4}{3} \pi \cdot 6 ^{3} = \frac{4}{3} \pi \cdot 216 = 288 \pi$

75% of this is

$288 \pi \cdot \frac{75}{100} = 216 \pi$

Report an Error

Example Question #222 : Geometry

Find the volume of a rectangular prism with the following information:

$\\height=5 \\length=4 \\width=3$

Possible Answers:

$\frac{20}{3}$

Correct answer:

Explanation:

The formula for volume of a rectangular prism is,

V=length*width*height .

For this problem, since

$\\height=5 \\length=4 \\width=3$

the solution would be

V=5*4*3=60 .

Report an Error

Example Question #223 : Geometry

What is the measure of a right angle?

Possible Answers:

180

360

Correct answer:

Explanation:

The measure of a right angle is degrees.

Report an Error

Example Question #224 : Geometry

Triangle_a

Figure NOT drawn to scale.

If $w = 125^{\circ }$ and $x = 81^{\circ }$ , evaluate .

Possible Answers:

More information is needed to solve the problem.

$55^{\circ }$

$53^{\circ }$

$44^{\circ }$

$35^{\circ}$

Correct answer:

$44^{\circ }$

Explanation:

The measure of an exterior angle of a triangle is the sum of the measures of its remote interior angles, so

w = x + y

$y = w - x= 125 - 81 = 44^{\circ }$

Report an Error

Example Question #1 : How To Find An Angle In An Acute / Obtuse Triangle

Triangle_a

Figure NOT drawn to scale.

If $x = 72^{\circ }$ and $y = 43^{\circ }$ , evaluate .

Possible Answers:

$65^{\circ}$

$108^{\circ}$

$125^{\circ }$

$137^{\circ}$

$115^{\circ }$

Correct answer:

$115^{\circ }$

Explanation:

The measure of an exterior angle of a triangle is the sum of the measures of its remote interior angles, so

$w = x + y = 72 + 43 = 115 ^{\circ }$

Report an Error

Example Question #225 : Geometry

If the vertex angle of an isoceles triangle is $64^{\circ}$ , what is the value of one of its base angles?

Possible Answers:

$64^{\circ}$

$116^{\circ}$

$36^{\circ}$

$58^{\circ}$

$26^{\circ}$

Correct answer:

$58^{\circ}$

Explanation:

In an isosceles triangle, the base angles are the same. Also, the three angles of a triangle add up to $180^{\circ}$ .

So, subtract the vertex angle from $180^{\circ}$ . You get $116^{\circ}$ .

Because there are two base angles you divide $116^{\circ}$ by , and you get $58^{\circ}$ .

Report an Error

Example Question #1411 : Concepts

Triangle

Note: Figure NOT drawn to scale.

Refer to the above diagram.

$45^{\circ } \leq m \angle 1 \leq 50^{\circ }$

$60^{\circ } \leq m \angle 2 \leq 70 ^{\circ }$

Which of the following could be a measure of $\angle 3$ ?

Possible Answers:

$125^{\circ }$

$100^{\circ }$

$130^{\circ }$

All of the other choices give a possible measure of $\angle 3$ .

$110^{\circ }$

Correct answer:

$110^{\circ }$

Explanation:

The measure of an exterior angle of a triangle is the sum of the measures of its remote interior angles, so

$\angle 3 = \angle 1 + \angle 2$ .

We also have the following constraints:

$45^{\circ } \leq m \angle 1 \leq 50^{\circ }$

$60^{\circ } \leq m \angle 2 \leq 70 ^{\circ }$

Then, by the addition property of inequalities,

$45^{\circ } + 60 ^{\circ }\leq m \angle 1 +m \angle 2 \leq 50^{\circ } + 70 ^{\circ }$

$105 ^{\circ }\leq m \angle 3 \leq 120^{\circ }$

Therefore, the measure of $\angle 3$ must fall in that range. Of the given choices, only $110^{\circ }$ falls in that range.

Report an Error

Example Question #2 : How To Find An Angle In An Acute / Obtuse Triangle

Triangle

Refer to the above diagram.

$45^{\circ } \leq m \angle 1 \leq 50^{\circ }$

$130^{\circ } \leq m \angle 3 \leq 140 ^{\circ }$

Which of the following could be a measure of $\angle 2$ ?

Possible Answers:

$85 ^{\circ }$

All of the other responses are correct.

$95 ^{\circ }$

$80 ^{\circ }$

$90 ^{\circ }$

Correct answer:

All of the other responses are correct.

Explanation:

The measure of an exterior angle of a triangle is the sum of the measures of its remote interior angles, so

$\angle 3 = \angle 1 + \angle 2$

$\angle 2 = \angle 3 - \angle 1$

Therefore, the maximum value of $\angle 2$ is the least possible value of $\angle 1$ subtracted from the greatest possible value of $\angle 3$ :

$140^{\circ } - 45^{\circ } = 95 ^{\circ }$

The minimum value of $\angle 2$ is the greatest possible value of $\angle 1$ subtracted from the least possible value of $\angle 3$ :

$130^{\circ } - 50^{\circ } = 80 ^{\circ }$

Therefore,

$80^{\circ } \leq \angle 2 \leq 95^{\circ }$

Since all of the choices fall in this range, all are possible measures of $\angle 2$ .

Report an Error

Example Question #1 : How To Find An Angle In A Right Triangle

One angle of a right triangle has measure $120^{\circ }$ . Give the measures of the other two angles.

Possible Answers:

$90^{\circ }, 120^{\circ }$

$30^{\circ }, 90^{\circ }$

$30^{\circ }, 30^{\circ }$

This triangle cannot exist.

$120^{\circ }, 120^{\circ }$

Correct answer:

This triangle cannot exist.

Explanation:

A right triangle must have one right angle and two acute angles; this means that no angle of a right triangle can be obtuse. But since $120^{\circ } > 90^{\circ }$ , it is obtuse. This makes it impossible for a right triangle to have a $120^{\circ }$ angle.

Report an Error

Example Question #1 : How To Find An Angle In A Right Triangle

One angle of a right triangle has measure $68^{\circ }$ . Give the measures of the other two angles.

Possible Answers:

This triangle cannot exist.

$44^{\circ },68^{\circ }$

$56^{\circ },56^{\circ }$

$22^{\circ }, 90^{\circ }$

$52^{\circ }, 60^{\circ }$

Correct answer:

$22^{\circ }, 90^{\circ }$

Explanation:

One of the angles of a right triangle is by definition a right, or $90^{\circ }$ , angle, so this is the measure of one of the missing angles. Since the measures of the angles of a triangle total $180^{\circ }$ , if we let the measure of the third angle be , then:

x + 68 + 90 = 180

x + 158 = 180

x + 158 - 158= 180 - 158

x = 22

The other two angles measure $22 ^{\circ }, 90^{\circ }$ .

Report an Error

View Tutors

Ana
Certified Tutor

Grand Canyon University, Bachelors, Education. Grand Canyon University, Masters, Education.

View Tutors

Stephanie
Certified Tutor

Cleveland State University, Bachelor of Science, Mathematics. University of Portland, Masters in Education, Curriculum and In...

View Tutors

Martine
Certified Tutor

University of South Florida-Main Campus, Bachelors, Science. Windsor University School of Medicine, Doctor of Medicine, Scien...

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in Washington DC, ISEE Tutors in Seattle, French Tutors in Washington DC, SAT Tutors in Los Angeles, French Tutors in Boston, Math Tutors in Phoenix, French Tutors in San Diego, Math Tutors in New York City, Computer Science Tutors in Chicago, MCAT Tutors in New York City

Popular Courses & Classes

ISEE Courses & Classes in Boston, GRE Courses & Classes in Miami, GRE Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in New York City, LSAT Courses & Classes in Philadelphia, ISEE Courses & Classes in Los Angeles, GRE Courses & Classes in Los Angeles, SAT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Washington DC, SAT Courses & Classes in Boston

Popular Test Prep

MCAT Test Prep in Philadelphia, GRE Test Prep in New York City, SAT Test Prep in Seattle, ISEE Test Prep in Boston, ISEE Test Prep in Philadelphia, LSAT Test Prep in Atlanta, ISEE Test Prep in Phoenix, LSAT Test Prep in Philadelphia, LSAT Test Prep in New York City, MCAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

HSPT Math : Geometry

Study concepts, example questions & explanations for HSPT Math

All HSPT Math Resources

Example Questions

Example Question #221 : Geometry

Example Question #222 : Geometry

Example Question #223 : Geometry

Example Question #224 : Geometry

Example Question #1 : How To Find An Angle In An Acute / Obtuse Triangle

Example Question #225 : Geometry

Example Question #1411 : Concepts

Example Question #2 : How To Find An Angle In An Acute / Obtuse Triangle

Example Question #1 : How To Find An Angle In A Right Triangle

Example Question #1 : How To Find An Angle In A Right Triangle

All HSPT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: