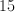All HSPT Math Resources
Example Questions
Example Question #1 : Geometry
A student creates a challenge for his friend. He first draws a square, the adds the line for each of the 2 diagonals. Finally, he asks his friend to draw the circle that has the most intersections possible.
How many intersections will this circle have?

Example Question #1 : Geometry
Two pairs of parallel lines intersect:

If A = 135o, what is 2*|B-C| = ?
160°
140°
150°
170°
180°
180°
By properties of parallel lines A+B = 180o, B = 45o, C = A = 135o, so 2*|B-C| = 2* |45-135| = 180o
Example Question #2 : Intersecting Lines And Angles
Lines 





Not enough information.
Since we know opposite angles are equal, it follows that angle 

Imagine a parallel line passing through point 




Example Question #3 : Geometry
If 


When the measure of an angle is added to the measure of its supplement, the result is always 180 degrees. Put differently, two angles are said to be supplementary if the sum of their measures is 180 degrees. For example, two angles whose measures are 50 degrees and 130 degrees are supplementary, because the sum of 50 and 130 degrees is 180 degrees. We can thus write the following equation:
Subtract 40 from both sides.
Add 
The answer is 
Example Question #1 : Geometry
In the following diagram, lines 



It cannot be determined
When two parallel lines are intersected by another line, the sum of the measures of the interior angles on the same side of the line is 180°. Therefore, the sum of the angle that is labeled as 100° and angle y is 180°. As a result, angle y is 80°.
Another property of two parallel lines that are intersected by a third line is that the corresponding angles are congruent. So, the measurement of angle x is equal to the measurement of angle y, which is 80°.
Example Question #251 : Geometry

Examine the above diagram. If 


The two marked angles are same-side exterior angles of parallel lines, which are supplementary - that is, their measures have sum 180. We can solve for 
Example Question #252 : Geometry

Examine the above diagram. If 


The two marked angles are same-side interior angles of parallel lines, which are supplementary - that is, their measures have sum 180. We can solve for 
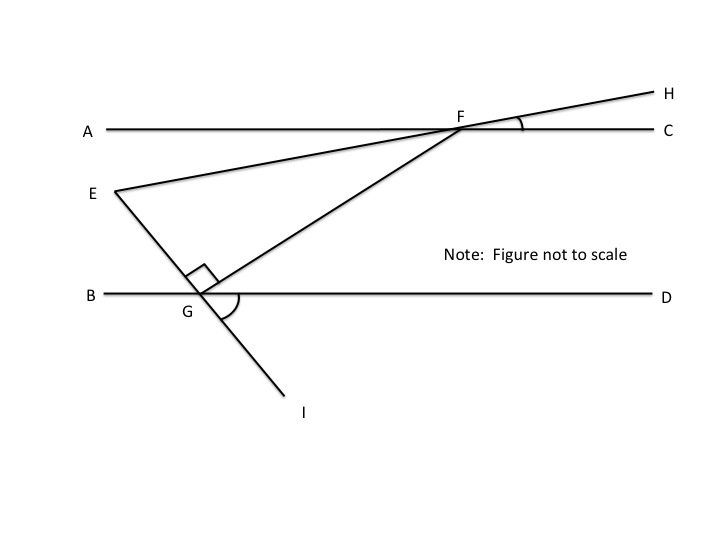
Example Question #1 : Lines

Examine the above diagram. What is 
By angle addition,
Example Question #1 : How To Find An Angle

Examine the above diagram. Which of the following statements must be true whether or not 


Four statements can be eliminated by the various parallel theorems and postulates. Congruence of alternate interior angles or corresponding angles forces the lines to be parallel, so


Also, if same-side interior angles or same-side exterior angles are supplementary, the lines are parallel, so


However, 

Example Question #1 : Lines





What is 
Supplementary angles and complementary angles have measures totaling 





Certified Tutor
All HSPT Math Resources