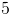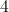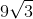Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Triangles

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : How To Find The Area Of A Right Triangle

Rt_triangle_letters

If $c=90^\circ$ , Y=4 , and Z=3 , what is the area of this triangle?

Possible Answers:

Correct answer:

Explanation:

The formula for area of a triangble is $A=\frac{1}{2}bh$ .

Since $c=90^\circ$ , will be the base and will be the height.

Plug in our given values to solve:

$A=\frac{1}{2}*4*3$

A=6

Report an Error

Example Question #4 : How To Find The Area Of A Right Triangle

Find the area of the following triangle:

Screen_shot_2014-03-01_at_9.07.42_pm

Possible Answers:

$2\sqrt{3} m^2$

$3\sqrt{3} m^2$

4 m^2

$3\sqrt{2} m^2$

6 m^2

Correct answer:

$2\sqrt{3} m^2$

Explanation:

The formula for the area of a right triangle is:

$A = \frac{1}{2} (b)(h)$

where is the length of the base and is the length of the height.

Use the formulas for a a 30-60-90 triangle to find the length of the base. The formula for a triangle is $a-a \sqrt{3}-2a$ .

Our 30-60-90 triangle is: $2m-2\sqrt{3}m-4m$

Plugging in our values, we get:

$A = \frac{1}{2} (2m)(2\sqrt{3}m) = 2\sqrt{3} m^2$

Report an Error

Example Question #5 : How To Find The Area Of A Right Triangle

Find the area of the following right triangle:

Screen_shot_2014-03-01_at_9.09.16_pm

Possible Answers:

64m^2

$32\sqrt{2}m^2$

16m^2

$16\sqrt{2}m^2$

32m^2

Correct answer:

16m^2

Explanation:

The formula for the area of a right triangle is:

$A = \frac{1}{2} (b)(h)$

where is the length of the base and is the length of the height.

Use the formulas for a 45-45-90 triangle to find the length of the base and height. The formula for a triangle is $a-a-a \sqrt{2}$

Our 45-45-90 triangle is: $4 \sqrt{2}m-4 \sqrt{2}m-8m$

Plugging in our values, we get:

$A = \frac{1}{2} (4\sqrt{2}m)(4\sqrt{2}m) = 16m^2$

Report an Error

Example Question #3 : How To Find The Area Of A Right Triangle

You are given a right triangle with legs of length feet and feet. What is the area of this triangle?

Possible Answers:

square feet

Correct answer:

square feet

Explanation:

Since we have a right triangle, and are given the lengths of the legs, we are by definition given the base and height. Recall that the legs of the triangle are those next to the right angle, and the hypotenuse is across from the right angle.

Recall the formula for the area of a triangle:

$Area = \frac{1}{2} \cdot base \cdot height$

Since we know the base and height we plug them into the equation above:

$Area = \frac{1}{2} \cdot 3 \cdot 4 = 6$

We are given units of feet, so the area will be in terms of square feet. Then, our answer is square feet.

Report an Error

Example Question #3 : How To Find The Area Of A Right Triangle

The ratio for the side lengths of a right triangle is 3:4:5. If the perimeter is 48, what is the area of the triangle?

Possible Answers:

108

240

Correct answer:

Explanation:

We can model the side lengths of the triangle as 3x, 4x, and 5x. We know that perimeter is 3x+4x+5x=48, which implies that x=4. This tells us that the legs of the right triangle are 3x=12 and 4x=16, therefore the area is A=1/2 bh=(1/2)(12)(16)=96.

Report an Error

Example Question #1 : How To Find The Area Of A Right Triangle

The length of one leg of an equilateral triangle is 6. What is the area of the triangle?

Possible Answers:

$9\sqrt{3}$

Correct answer:

$9\sqrt{3}$

Explanation:

$A=\frac{1}{2}(B)(H)$

The base is equal to 6.

The height of an quilateral triangle is equal to $\frac{B\sqrt{3}}{2}$ , where is the length of the base.

$A=\frac{1}{2}(6)(\frac{6\sqrt{3}}{2})=\frac{1}{2}(6)(3\sqrt{3})=9\sqrt{3}$

Report an Error

Example Question #1 : Right Triangles

Acute angles x and y are inside a right triangle. If x is four less than one third of 21, what is y?

Possible Answers:

Correct answer:

Explanation:

We know that the sum of all the angles must be 180 and we already know one angle is 90, leaving the sum of x and y to be 90.

Solve for x to find y.

One third of 21 is 7. Four less than 7 is 3. So if angle x is 3 then that leaves 87 for angle y.

Report an Error

Example Question #1 : Triangles

If a right triangle has one leg with a length of 4 and a hypotenuse with a length of 8, what is the measure of the angle between the hypotenuse and its other leg?

Possible Answers:

Correct answer:

Explanation:

The first thing to notice is that this is a 30^o:60^o:90^o triangle. If you draw a diagram, it is easier to see that the angle that is asked for corresponds to the side with a length of 4. This will be the smallest angle. The correct answer is 30.

Report an Error

Example Question #1 : How To Find An Angle In A Right Triangle

Triangle

In the figure above, what is the positive difference, in degrees, between the measures of angle ACB and angle CBD?

Possible Answers:

Correct answer:

Explanation:

In the figure above, angle ADB is a right angle. Because side AC is a straight line, angle CDB must also be a right angle.

Let’s examine triangle ADB. The sum of the measures of the three angles must be 180 degrees, and we know that angle ADB must be 90 degrees, since it is a right angle. We can now set up the following equation.

x + y + 90 = 180

Subtract 90 from both sides.

x + y = 90

Next, we will look at triangle CDB. We know that angle CDB is also 90 degrees, so we will write the following equation:

y – 10 + 2x – 20 + 90 = 180

y + 2x + 60 = 180

Subtract 60 from both sides.

y + 2x = 120

We have a system of equations consisting of x + y = 90 and y + 2x = 120. We can solve this system by solving one equation in terms of x and then substituting this value into the second equation. Let’s solve for y in the equation x + y = 90.

x + y = 90

Subtract x from both sides.

y = 90 – x

Next, we can substitute 90 – x into the equation y + 2x = 120.

(90 – x) + 2x = 120

90 + x = 120

x = 120 – 90 = 30

x = 30

Since y = 90 – x, y = 90 – 30 = 60.

The question ultimately asks us to find the positive difference between the measures of ACB and CBD. The measure of ACB = 2x – 20 = 2(30) – 20 = 40 degrees. The measure of CBD = y – 10 = 60 – 10 = 50 degrees. The positive difference between 50 degrees and 40 degrees is 10.

The answer is 10.

Report an Error

Example Question #1 : How To Find An Angle In A Right Triangle

Rt_triangle_letters If angle $b=35^\circ$ and angle $c=90^\circ$ , what is the value for angle ?

Possible Answers:

$55^\circ$

$45^\circ$

$35^\circ$

$17.5^\circ$

$90^\circ$

Correct answer:

$55^\circ$

Explanation:

For this problem, remember that the sum of the degrees in a triangle is $180^\circ$ .

That means that $a+b+c=180^\circ$ .

Plug in our given values to solve:

$a+35^\circ+90^\circ=180^\circ$

$a+125^\circ=180^\circ$

Subtract $125^\circ$ from both sides:

$a=55^\circ$

Report an Error

View Tutors

Pankaj
Certified Tutor

University of Delhi, Electrical Engineer, Electrical Engineering. Columbia University in the City of New York, Master of Arts...

View Tutors

Saarim
Certified Tutor

St Edwards University, Bachelor of Science, Mathematics.

View Tutors

Melissa
Certified Tutor

University of Houston, Bachelors, Political Science and Government.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ACT Tutors in Washington DC, SSAT Tutors in Denver, Spanish Tutors in San Francisco-Bay Area, GMAT Tutors in Phoenix, SAT Tutors in Chicago, Algebra Tutors in Washington DC, Spanish Tutors in Washington DC, SSAT Tutors in Boston, Reading Tutors in San Francisco-Bay Area, ISEE Tutors in Miami

Popular Courses & Classes

SAT Courses & Classes in Atlanta, Spanish Courses & Classes in Washington DC, MCAT Courses & Classes in Houston, Spanish Courses & Classes in New York City, Spanish Courses & Classes in Boston, Spanish Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in New York City, GRE Courses & Classes in Chicago, ACT Courses & Classes in Los Angeles, GMAT Courses & Classes in Washington DC

Popular Test Prep

MCAT Test Prep in San Francisco-Bay Area, ISEE Test Prep in Dallas Fort Worth, ACT Test Prep in Los Angeles, SAT Test Prep in Los Angeles, SAT Test Prep in Chicago, GRE Test Prep in Chicago, ISEE Test Prep in Chicago, ISEE Test Prep in Washington DC, SAT Test Prep in Philadelphia, GMAT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Triangles

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #2 : How To Find The Area Of A Right Triangle

Example Question #4 : How To Find The Area Of A Right Triangle

Example Question #5 : How To Find The Area Of A Right Triangle

Example Question #3 : How To Find The Area Of A Right Triangle

Example Question #3 : How To Find The Area Of A Right Triangle

Example Question #1 : How To Find The Area Of A Right Triangle

Example Question #1 : Right Triangles

Example Question #1 : Triangles

Example Question #1 : How To Find An Angle In A Right Triangle

Example Question #1 : How To Find An Angle In A Right Triangle

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: