High School Math : Triangles
Study concepts, example questions & explanations for High School Math
All High School Math Resources
Example Questions
Example Question #1 : Apply The Pythagorean Theorem To Find The Distance Between Two Points In A Coordinate System: Ccss.Math.Content.8.G.B.8
Angela drives 30 miles north and then 40 miles east. How far is she from where she began?
50 miles
45 miles
60 miles
35 miles
50 miles
By drawing Angela’s route, we can connect her end point and her start point with a straight line and will then have a right triangle. The Pythagorean theorem can be used to solve for how far she is from the starting point: a2+b2=c2, 302+402=c2, c=50. It can also be noted that Angela’s route represents a multiple of the 3-4-5 Pythagorean triple.
Example Question #5 : Apply The Pythagorean Theorem To Find The Distance Between Two Points In A Coordinate System: Ccss.Math.Content.8.G.B.8
To get from his house to the hardware store, Bob must drive 3 miles to the east and then 4 miles to the north. If Bob was able to drive along a straight line directly connecting his house to the store, how far would he have to travel then?
Since east and north directions are perpendicular, the possible routes Bob can take can be represented by a right triangle with sides a and b of length 3 miles and 5 miles, respectively. The hypotenuse c represents the straight line connecting his house to the store, and its length can be found using the Pythagorean theorem: c2 = 32+ 42 = 25. Since the square root of 25 is 5, the length of the hypotenuse is 5 miles.
Example Question #53 : Plane Geometry
A park is designed to fit within the confines of a triangular lot in the middle of a city. The side that borders Elm street is 15 feet long. The side that borders Broad street is 23 feet long. Elm street and Broad street meet at a right angle. The third side of the park borders Popeye street, what is the length of the side of the park that borders Popeye street?
27.46 feet
17.44 feet
22.5 feet
16.05 feet
18.5 feet
27.46 feet
This question requires the use of Pythagorean Theorem. We are given the length of two sides of a triangle and asked to find the third. We are told that the two sides we are given meet at a right angle, this means that the missing side is the hypotenuse. So we use a2 + b2 = c2, plugging in the two known lengths for a and b. This yields an answer of 27.46 feet.
Example Question #42 : Right Triangles
A right triangle has legs of 15m and 20m. What is the length of the hypotenuse?
45m
30m
35m
40m
25m
25m
The Pythagorean theorem is a2 + b2 = c2, where a and b are legs of the right triangle, and c is the hypotenuse.
(15)2 + (20)2 = c2 so c2 = 625. Take the square root to get c = 25m
Example Question #41 : Triangles
Paul leaves his home and jogs 3 miles due north and 4 miles due west. If Paul could walk a straight line from his current position back to his house, how far, in miles, is Paul from home?
√14
7
5
4
25
5
By using the Pythagorean Theorem, we can solve for the distance “as the crow flies” from Paul to his home:
32 + 42 = x2
9 + 16 = x2
25 = x2
5 = x
Example Question #43 : Right Triangles
Given a right triangle where the two legs have lengths of 3 and 4 respectively, what is the length of the hypotenuse?
4
5
25
9
3
5
The hypotenuse can be found using Pythagorean Theorem, which is a2 + b2 = c2, so we plug in a = 3 and b = 4 to get c.
c2 =25, so c = 5
Example Question #61 : Plane Geometry
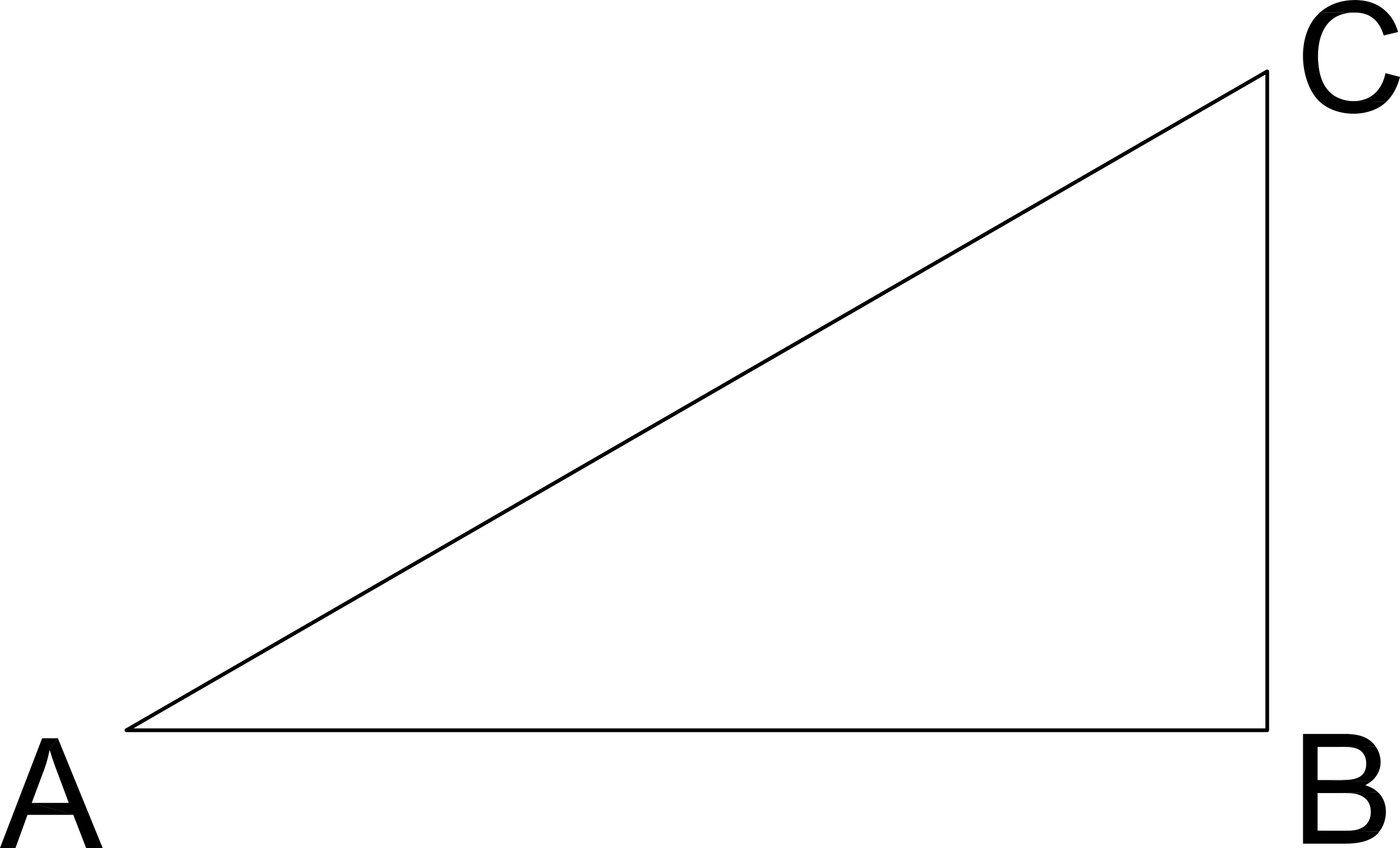
Length AB = 4
Length BC = 3
If a similar triangle has a hypotenuse length of 25, what are the lengths of its two legs?
20 and 25
15 and 25
3 and 4
5 and 25
15 and 20
15 and 20
Similar triangles are in proportion.
Use Pythagorean Theorem to solve for AC:
Pythagorean Theorem: AB2 + BC2 = AC2
42 + 32 = AC2
16 + 9 = AC2
25 = AC2
AC = 5
If the similar triangle's hypotenuse is 25, then the proportion of the sides is AC/25 or 5/25 or 1/5.
Two legs then are 5 times longer than AB or BC:
5 * (AB) = 5 * (4) = 20
5 * (BC) = 5 * (3) = 15
Example Question #51 : Triangles
If the base of a right triangle is 5 cm long and the height of the triangle is 7 cm longer than the base, what is the length of the third side of the triangle in cm?
Find the height of the triangle
Use the Pythagorean Theorem to solve for the length of the third side, or hypotenuse.
Example Question #52 : Triangles
Given the right triangle in the diagram, what is the length of the hypotenuse?
To find the length of the hypotenuse use the Pythagorean Theorem:
Where 
The hypotenuse is 10 inches long.
Example Question #53 : Triangles
Triangle ABC is a right triangle. If the length of side A = 3 inches and C = 5 inches, what is the length of side B?
6 inches
1 inches
1/2 inches
4.5 inches
4 inches
4 inches
Using the Pythagorean Theorem, we know that 
This gives:
Subtracting 9 from both sides of the equation gives:
All High School Math Resources
