To find the perimeter of a triangle you must add all of the side lengths together. 

In this case our equation would look like 

Add the numbers together to get the answer .

Drawing points gives sides of a right triangle of 4, 5, and an unknown hypotenuse.

Using the pythagorean theorem we find that the hypotenuse is .

The formula for the perimeter of a right triangle is:

where  is the length of a side.

Use the formulas for a a  triangle to find the length of the base. The formula for a  triangle is .

Our  triangle is: 

Plugging in our values, we get:

The formula for the perimeter of a right triangle is:

where  is the length of a side.

Use the formulas for a  triangle to find the length of the base and height. The formula for a  triangle is 

Our  triangle is: 

Plugging in our values, we get:

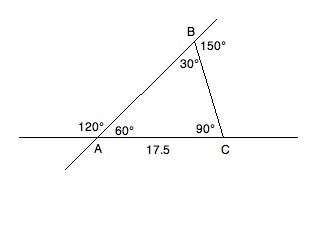
Consult the diagram above while reading the solution. Because of what we know about supplementary angles, we can fill in the inner values of the triangle. Angles A and B can be found by the following reductions:

A + 120 = 180; A = 60

B + 150 = 180; B = 30

Since we know A + B + C = 180 and have the values of A and B, we know:

60 + 30 + C = 180; C = 90

This gives us a 30:60:90 triangle. Now, since 17.5 is across from the 30° angle, we know that the other two sides will have to be √3 and 2 times 17.5; therefore, our perimeter will be as follows:

The area of a triangle is denoted by the equation 1/2 b x h.

b stands for the length of the base, and h stands for the height.

Here we are told that the perimeter (total length of all three sides) is 12, and the hypotenuse (the side that is neither the height nor the base) is 5 units long.

So, 12-5 = 7 for the total perimeter of the base and height.

7 does not divide cleanly by two, but it does break down into 3 and 4,

and 1/2 (3x4) yields 6.

Another way to solve this would be if you recall your rules for right triangles, one of the very basic ones is the 3,4,5 triangle, which is exactly what we have here

Because the perimeter is equal to the sum of the lengths of the three sides of a triangle, we can add the three expressions for the lengths and set them equal to 40.

Perimeter:

Simplify the x terms.

Simplify the constants.

Subtract 8 from both sides.

Divide by 4

One side is 8.

The second side is

.

The third side is

.

Thus, the sides of the triangle are 8, 15, and 17.

The question asks us for the area of the triangle, which is given by the formula (1/2)bh. We are told it is a right triangle, so we can use one of the legs as the base, and the other leg as the height, since the legs will intersect at right angles. The legs of the right triangle must be the smallest sides (the longest must be the hypotenuse), which in this case are 8 and 15. So, let's assume that 8 is the base and 15 is the height. 

The area of a triangle is (1/2)bh. We can substitute 8 and 15 for b and h.

.

The answer is 60 units squared.

Because PA and PB are tangent to circle O, angles PAO and PBO must be right angles; therefore, triangles PAO and PBO are both right triangles.

Since AO and OB are both radii of circle O, they are congruent. Furthermore, because PA and PB are external tangents originating from the same point, they must also be congruent.

So, in triangles PAO and PBO, we have two sides that are congruent, and we have a congruent angle (all right angles are congruent) between them. Therefore, by the Side-Angle-Side (SAS) Theorem of congruency, triangles PAO and PBO are congruent.

Notice that quadrilateral PAOB can be broken up into triangles PAO and PBO. Since those triangles are congruent, each must comprise one half of the area of quadrilateral PAOB. As a result, if we find the area of one of the triangles, we can double it in order to find the area of the quadrilateral.

Let's determine the area of triangle PAO. We have already established that it is a right triangle. We are told that PO, which is the hypotenuse of the triangle, is equal to 17. We are also told that the diameter of circle O is 16, which means that every radius of the circle is 8, because a radius is half the size of a diameter. Since segment AO is a radius, its length must be 8.

So, triangle PAO is a right triangle with a hypotenuse of 17 and a leg of 8. We can use the Pythagorean Theorem in order to find the other leg. According to the Pythagorean Theorem, if a and b are the lengths of the legs of a right triangle, and c is the length of the hypotenuse, then:

a² + b² = c²

Let us let b represent the length of PA.

8² + b² = 17²

64 + b² = 289

Subtract 64 from both sides.

b² = 225

Take the square root of both sides.

b = 15

This means that the length of PA is 15.

Now let's apply the formula for the area of a right triangle. Because the legs of a right triangle are perpendicular, one can be considered the base, and the other can be considered the height of the triangle.

area of triangle PAO = (¹/₂)bh

= (¹/₂)(8)(15) = 60

Ultimately, we must find the area of quadrilateral PAOB; however, we previously determined that triangles PAO and PBO each comprise half of the quadrilateral. Thus, if we double the area of PAO, we would get the area of quadrilateral PAOB.

Area of PAOB = 2(area of PAO)

= 2(60) = 120 square units

The answer is 120.

The answer is 12. In this circumstance, the area of the triangle cannot be smaller than its hypotenuse length, and cannot be bigger than its hypotenuse squared (that would be the area of a square).

Drawing a quick sketch of this triangle will reveal that it is a right triangle. The lines AB and AC form the height and base of this triangle interchangeably, depending on how you look at it.

Either way the formula for the area of the triangle is the distance from A to B multiplied by the distance from A to C, divided by 2.

This is