We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #42 : Right Triangles

Given a right triangle where the two legs have lengths of 3 and 4 respectively, what is the length of the hypotenuse?

Possible Answers:

Correct answer:

Explanation:

The hypotenuse can be found using Pythagorean Theorem, which is a²+ b²= c², so we plug in a = 3 and b = 4 to get c.

c²=25, so c = 5

Report an Error

Example Question #484 : Geometry

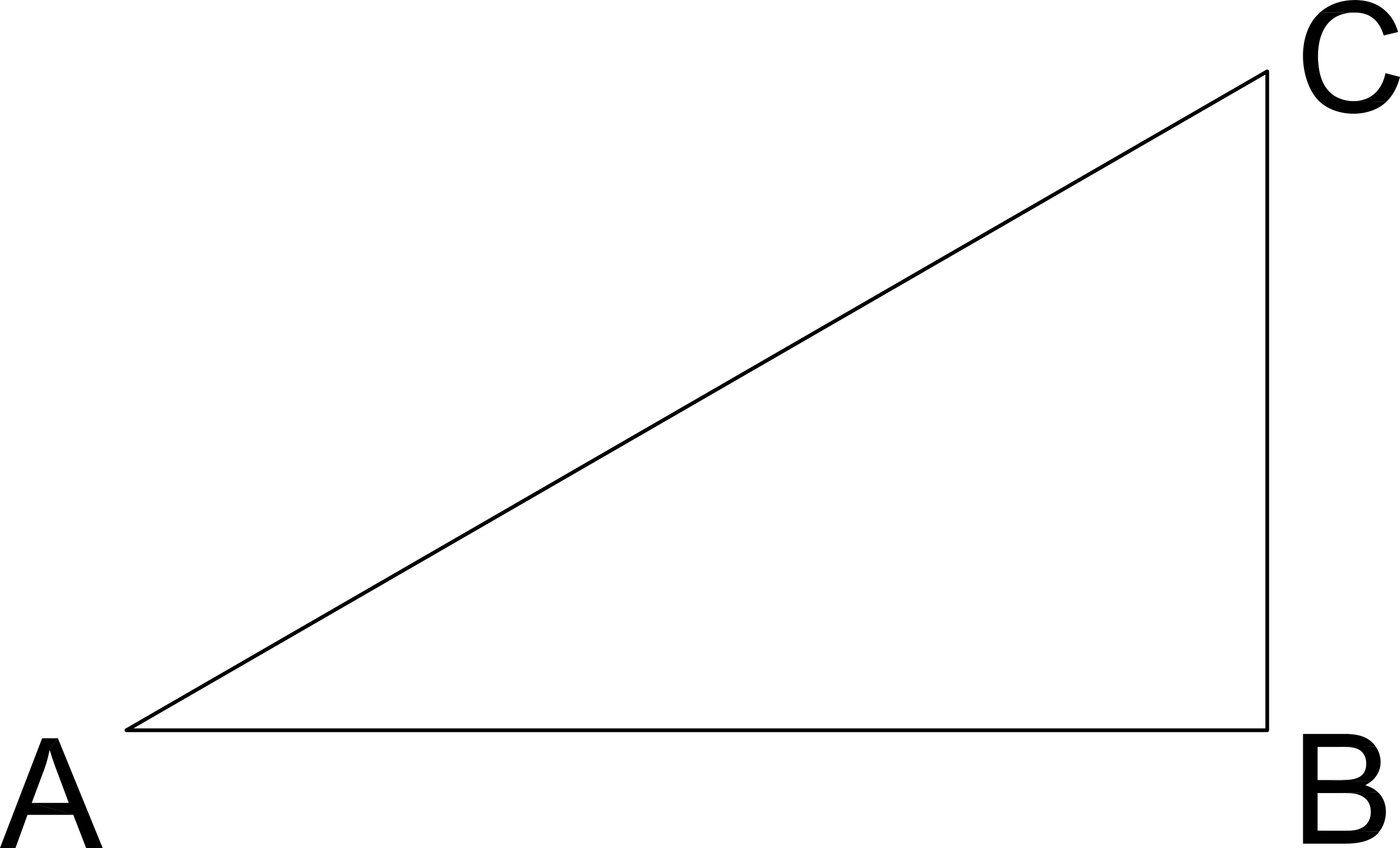
Triangle

Length AB = 4

Length BC = 3

If a similar triangle has a hypotenuse length of 25, what are the lengths of its two legs?

Possible Answers:

3 and 4

5 and 25

15 and 25

15 and 20

20 and 25

Correct answer:

15 and 20

Explanation:

Similar triangles are in proportion.

Use Pythagorean Theorem to solve for AC:

Pythagorean Theorem: AB² + BC² = AC²

4² + 3² = AC²

16 + 9 = AC²

25 = AC²

AC = 5

If the similar triangle's hypotenuse is 25, then the proportion of the sides is AC/25 or 5/25 or 1/5.

Two legs then are 5 times longer than AB or BC:

5 * (AB) = 5 * (4) = 20

5 * (BC) = 5 * (3) = 15

Report an Error

Example Question #481 : Psat Mathematics

If the base of a right triangle is 5 cm long and the height of the triangle is 7 cm longer than the base, what is the length of the third side of the triangle in cm?

Possible Answers:

Correct answer:

Explanation:

Find the height of the triangle 5 + 7 = 12

Use the Pythagorean Theorem to solve for the length of the third side, or hypotenuse.

$c^{2} = a^{2} + b^{2}$

$c^{2} = 5^{2} + 12^{2}$

$c^{2} = 25 + 144 = 169$

c = 13

Report an Error

Example Question #33 : Right Triangles

Given the right triangle in the diagram, what is the length of the hypotenuse?

Possible Answers:

$12\ in$

$7\ in$

$20\ in$

$14\ in$

$10\ in$

Correct answer:

$10\ in$

Explanation:

To find the length of the hypotenuse use the Pythagorean Theorem: $a^{2}+b^{2}=c^{2}$

Where and are the legs of the triangle, and is the hypotenuse.

$6^{2}+8^{2}=100$

$(100)^{\frac{1}2}=10$

The hypotenuse is 10 inches long.

Report an Error

Example Question #486 : Geometry

Righttriangle

Triangle ABC is a right triangle. If the length of side A = 3 inches and C = 5 inches, what is the length of side B?

Possible Answers:

1/2 inches

1 inches

6 inches

4 inches

4.5 inches

Correct answer:

4 inches

Explanation:

Using the Pythagorean Theorem, we know that $a^{2} + b^{2} = c^{2}$ .

This gives:

$3^{2} + b^{2} = 5^{2}$

$9 + b^{2} = 25$

Subtracting 9 from both sides of the equation gives:

$b^{2} = 16$

b = 4 inches

Righttriangle

Report an Error

Example Question #482 : Psat Mathematics

Righttriangle

Triangle ABC is a right triangle. If the length of side A = 8 inches and B = 11 inches, find the length of the hypoteneuse (to the nearest tenth).

Possible Answers:

185 inches

13.7 inches

14.2 inches

13.6 inches

184 inches

Correct answer:

13.6 inches

Explanation:

Using the Pythagrean Theorem, we know that $a^{2} + b^{2} = c^{2}$ .

This tells us:

$8^{2} + 11^{2} = C^{2}$

$64 + 121 = C^{2}$

$185 = C^{2}$

Taking the square root of both sides, we find that C = 13.6 inches

Report an Error

Example Question #55 : Triangles

Righttriangle

Given:

A = 6 feet

B = 9 feet

What is the length of the hypoteneuse of the triangle (to the nearest tenth)?

Possible Answers:

10.6 feet

10.8 feet

10.5 feet

10.2 feet

10.1 feet

Correct answer:

10.8 feet

Explanation:

Using the Pythagrean Theorem, we know that $a^{2} + b^{2} = c^{2}$ .

This tells us:

$6^{2} + 9^{2} = C^{2}$

$36 + 81 = C^{2}$

$117 = C^{2}$

Taking the square root of both sides, we find that C = 10.8

Report an Error

Example Question #21 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

Righttriangle

Given:

A = 2 miles

B = 3 miles

What is the length of the hypoteneuse of triangle ABC, to the nearest tenth?

Possible Answers:

3.5 miles

3.4 miles

3.7 miles

3.2 miles

3.6 miles

Correct answer:

3.6 miles

Explanation:

Using the Pythagrean Theorem, we know that $a^{2} + b^{2} = c^{2}$ .

This tells us:

$2^{2} + 3^{2} = C^{2}$

$4 + 9 = C^{2}$

$13 = C^{2}$

Taking the square root of both sides, we find that C = 3.6

Report an Error

Example Question #491 : Geometry

Given that two sides of a right triangle measure 2 feet and 3 feet, respectively, with a hypoteneuse of x, what is the perimeter of this right triangle (to the nearest tenth)?

Possible Answers:

9.4 feet

8.6 feet

18 feet

3.6 feet

6.4 feet

Correct answer:

8.6 feet

Explanation:

Using the Pythagrean Theorem, we know that $a^{2} + b^{2} = c^{2}$ .

This tells us:

$2^{2} + 3^{2} = C^{2}$

$4 + 9 = C^{2}$

$13 = C^{2}$

Taking the square root of both sides, we find that C = 3.6

To find the perimeter, we add the side lengths together, which gives us that the perimeter is: 3 + 2 + 3.6 = 8.6

Report an Error

Example Question #492 : Geometry

$In\;\Delta GHJ, \;what\;is\;the\;length\;of\;\overline{GJ}?$

Possible Answers:

Correct answer:

Explanation:

$Use\;the\;Pythagorean\;Theorem:A^2+B^2=C^2,\;to\; find\;\overline{GJ}.$

5^2+12^2=C^2

25+144=C^2

169=C^2

$C=\sqrt{169}=13$

Report an Error

View Tutors

Angelica
Certified Tutor

Morehead State University, Bachelor in Arts, Political Science and Government.

View Tutors

Jessica
Certified Tutor

Eastern Kentucky University, Bachelor in Arts, English.

View Tutors

Eva
Certified Tutor

Technicka Univerzita Liberec, Bachelor of Education, Education.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in New York City, SAT Tutors in San Francisco-Bay Area, Spanish Tutors in Boston, Spanish Tutors in Phoenix, French Tutors in Phoenix, GMAT Tutors in Philadelphia, Statistics Tutors in New York City, Statistics Tutors in Denver, Physics Tutors in Dallas Fort Worth, Statistics Tutors in Chicago

Popular Courses & Classes

SAT Courses & Classes in Phoenix, MCAT Courses & Classes in Washington DC, ISEE Courses & Classes in Houston, ACT Courses & Classes in San Diego, SSAT Courses & Classes in Atlanta, GRE Courses & Classes in Miami, Spanish Courses & Classes in Miami, Spanish Courses & Classes in Washington DC, SAT Courses & Classes in Washington DC, MCAT Courses & Classes in Seattle

Popular Test Prep

ISEE Test Prep in Phoenix, ISEE Test Prep in Chicago, SSAT Test Prep in Boston, GMAT Test Prep in Denver, GMAT Test Prep in Washington DC, SAT Test Prep in Houston, ISEE Test Prep in San Francisco-Bay Area, ACT Test Prep in Boston, GMAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #42 : Right Triangles

Example Question #484 : Geometry

Example Question #481 : Psat Mathematics

Example Question #33 : Right Triangles

Example Question #486 : Geometry

Example Question #482 : Psat Mathematics

Example Question #55 : Triangles

Example Question #21 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

Example Question #491 : Geometry

Example Question #492 : Geometry

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: