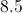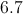High School Math : High School Math
Study concepts, example questions & explanations for High School Math
All High School Math Resources
Example Questions
Example Question #1 : How To Find The Area Of A Rectangle
The front façade of a building is 100 feet tall and 40 feet wide. There are eight floors in the building, and each floor has four glass windows that are 8 feet wide and 6 feet tall along the front façade. What is the total area of the glass in the façade?
768 ft2
2464 ft2
1536 ft2
192 ft2
1536 ft2
1536 ft2
Glass Area per Window = 8 ft x 6 ft = 48 ft2
Total Number of Windows = Windows per Floor * Number of Floors = 4 * 8 = 32 windows
Total Area of Glass = Area per Window * Total Number of Windows = 48 * 32 = 1536 ft2
Example Question #1 : How To Find The Area Of A Rectangle
Mark is making a plan to build a rectangular garden. He has 160 feet of fence to form the outside border of the garden. He wants the dimensions to look like the plan outlined below:
What is the area of the garden, rounded to the nearest square foot?
Perimeter: Sum of the sides:
4x + 4x + 2x+8 +2x+8 = 160
12x + 6 = 160
12x = 154
x =
Therefore, the short side of the rectangle is going to be:
And the long side is going to be:
The area of the rectangle is going to be as follows:
Area = lw
Example Question #41 : Rectangles
Two circles of a radius of 
The area of a square =
The area of a circle is
Area = Area of Square 
Example Question #651 : Geometry
If the area Rectangle A is 
Example Question #581 : High School Math
Erin is getting ready to plant her tulip garden. She wants to plant two tulips per square foot of garden. If her rectangular garden is enclosed by 24 feet of fencing, and the length of the fence is twice as long as its width, how many tulips will Erin plant?
48
32
16
24
64
64
We know that the following represents the formula for the perimeter of a rectangle:
In this particular case, we are told that the length of the fence is twice as long as the width. We can write this as the following expression:
Use this information to substitute in a variable for the length that matches the variable for width in our perimeter equation.
We also know that the length is two times the width; therefore, we can write the following:
The area of a rectangle is found by using this formula:
The area of the garden is 32 square feet. Erin will plant two tulips per square foot; thus, she will plant 64 tulips.
Example Question #582 : High School Math
What is the length of a diagonal of a square with a side length 
A square is comprised of two 45-45-90 right triangles. The hypotenuse of a 45-45-90 right triangle follows the rule below, where 
In this instance, 
Example Question #583 : High School Math
A square has sides of 
To find the diagonal of the square, we effectively cut the square into two 
The pattern for the sides of a 
Since two sides are equal to 
Therefore, the diagonal (the hypotenuse) will have a length of 
Example Question #584 : High School Math
A square has sides of 
To find the diagonal of the square, we effectively cut the square into two 
The pattern for the sides of a 
Since two sides are equal to 
Therefore, the diagonal (the hypotenuse) will have a length of 
Example Question #585 : High School Math
What is the length of the diagonal of a square with a side length of 
To find the diagonal of a square, we must use the side length to create a 90 degree triangle with side lengths of 
Pythagorean’s Theorem states 
Take 
After squaring the numbers, add them together:
Once you have the sum, take the square root of both sides:
Simplify to find the answer: 
Example Question #586 : High School Math
What is the length of the diagonal of a 7-by-7 square? (Round to the nearest tenth.)
To find the diagonal of a square we must use the side lengths to create a 90 degree triangle with side lengths of 7 and a hypotenuse which is equal to the diagonal.
We can use the Pythagorean Theorem here to solve for the hypotenuse of a right triangle.
The Pythagorean Theorem states
Plug the side lengths into the equation as 
Square the numbers:
Add the terms on the left side of the equation together:
Take the square root of both sides:
Therefore the length of the diagonal is 9.9.
Certified Tutor
Certified Tutor
All High School Math Resources
