All High School Math Resources
Example Questions
Example Question #401 : Act Math
A square garden has an area of 64 square feet. If you add 3 feet to each side, what is the new perimeter of the garden?
44
20
25
121
32
44
By finding the square root of the area of the garden, you find the length of one side, which is 8. We add 3 feet to this, giving us 11, then multiply this by 4 to get 44 feet for the perimeter.
Example Question #13 : Squares
The area of the shaded region of a square is 18. What is the perimeter of the square?
24
20
28
36
24
The area of the shaded region, which covers half of the square is 18 meaning that the total area of the square is 18 x 2, or 36. The area of a square is equal to the length of one side squared. Since the square root of 36 is 6, the length of 1 side is 6. The perimeter is the length of 1 side times 4 or 6 x 4.
Example Question #851 : Plane Geometry
The area of a square is 
The area of a square is given by 

Example Question #611 : High School Math
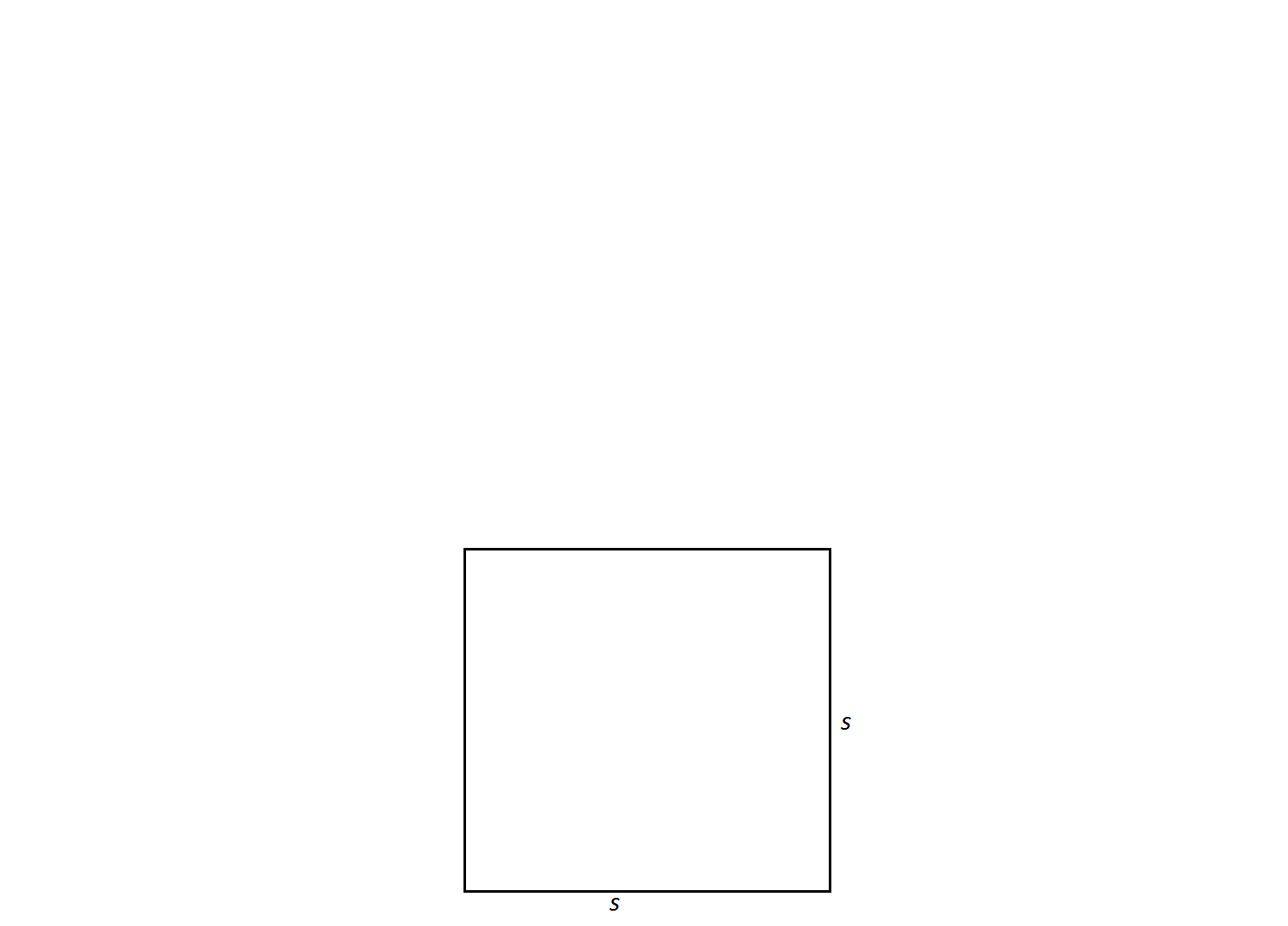
A square has a side length of 
Not enough information to solve
In order to find the perimeter of a square, one must add up all of its side lengths. The side lengths of a square are all equal; therefore, the formula for the perimeter of a square is 
Remember perimeter should be expressed in single units not units squared. Thus, 
Example Question #3 : How To Find The Perimeter Of A Square
The diagonal of a square has a length of 10 inches. What is the perimeter of the square in inches squared?
Using the Pythagorean Theorem, we can find the edge of a side to be √50, by 2a2=102. This can be reduced to 5√2. This can then be multiplied by 4 to find the perimeter.
Example Question #1 : How To Find The Length Of The Side Of A Square
The area of square R is 12 times the area of square T. If the area of square R is 48, what is the length of one side of square T?
16
4
2
1
2
We start by dividing the area of square R (48) by 12, to come up with the area of square T, 4. Then take the square root of the area to get the length of one side, giving us 2.
Example Question #621 : Psat Mathematics
When the side of a certain square is increased by 2 inches, the area of the resulting square is 64 sq. inches greater than the original square. What is the length of the side of the original square, in inches?
17
15
18
14
16
15
Let x represent the length of the original square in inches. Thus the area of the original square is x2. Two inches are added to x, which is represented by x+2. The area of the resulting square is (x+2)2. We are given that the new square is 64 sq. inches greater than the original. Therefore we can write the algebraic expression:
x2 + 64 = (x+2)2
FOIL the right side of the equation.
x2 + 64 = x2 + 4x + 4
Subtract x2 from both sides and then continue with the alegbra.
64 = 4x + 4
64 = 4(x + 1)
16 = x + 1
15 = x
Therefore, the length of the original square is 15 inches.
If you plug in the answer choices, you would need to add 2 inches to the value of the answer choice and then take the difference of two squares. The choice with 15 would be correct because 172 -152 = 64.
Example Question #611 : High School Math
If the area of a square is 25 inches squared, what is the perimeter?
Not enough information
25
20
15
10
20
The area of a square is equal to length times width or length squared (since length and width are equal on a square). Therefore, the length of one side is 

Example Question #1 : How To Find The Length Of The Side Of A Square

A square is inscribed inside a circle, as illustrated above. The radius of the circle is 






Given that the square's diagonals pass through the circle's center, those diagonals must each form a diameter of the circle. The circle's diameter is twice its radius, i.e. 






Example Question #612 : High School Math
Find the perimeter of a triangle with sides
Add up all of the sides to get 35 inches.
Certified Tutor
Certified Tutor
All High School Math Resources




























