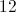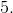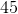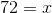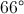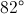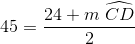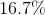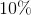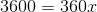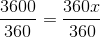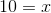High School Math : High School Math
Study concepts, example questions & explanations for High School Math
All High School Math Resources
Example Questions
Example Question #12 : Geometry
What is the measure of one exterior angle of a regular seventeen-sided polygon (nearest tenth of a degree)?
The sum of the measures of the exterior angles of any polygon, one per vertex, is 
Example Question #13 : Geometry
What is the measure of one exterior angle of a regular twenty-three-sided polygon (nearest tenth of a degree)?
The sum of the measures of the exterior angles of any polygon, one per vertex, is 
Example Question #4 : How To Find An Angle In A Polygon
What is the measure of one interior angle of a regular twenty-three-sided polygon (nearest tenth of a degree)?
The measure of each interior angle of a regular polygon with 
Example Question #5 : How To Find An Angle In A Polygon
A regular polygon has interior angles which measure 
The easiest way to answer this is to note that, since an interior angle and an exterior angle form a linear pair - and thus, a supplementary pair - each exterior angle would have measure 
Solve for 
The polygon has 20 sides.
Example Question #1 : How To Find The Length Of A Side Of A Polygon
If the area of a regular octagon is 160 and the apothem is 8, what is the side length?
To find the side length from the area of an octagon and the apothem we must use the area of a polygon which is
First plug in our numbers for area and the apothem to get
Then multiply to get
Then divide both sides by 4 to get the perimeter of the figure.
When we have the perimeter of a regular polygon, to find the side length we must divide by the number of sides of the polygon, in this case 8.
After dividing we find the side length is
Example Question #1 : Circles
A sector comprises 20% of a circle. What is the central angle of the sector?
Proporations can be used to solve for the central angle. Let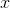 
Cross mulitply:
Solve for 
Example Question #1 : How To Find The Angle For A Percentage Of A Circle
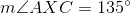
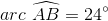
Find the degree measure of 
Not enough information is given to answer this question.
When two chords of a circle intersect, the measure of the angle they form is half the sum of the measures of the arcs they intercept. Therefore,
Since 
Substitute 
Example Question #1 : Circles
Two pizzas are made to the same dimensions. The only difference is that Pizza 1 is cut into pieces at 30° angles and Pizza 2 is cut at 45° angles. They are sold by the piece, the first for $1.95 per slice and the second for $2.25 per slice. What is the difference in total revenue between Pizza 2 and Pizza 1?
–$2.70
–$5.40
$0
$5.40
$2.70
–$5.40
First, let's calculate how many slices there are per pizza. This is done by dividing 360° by the respective slice degrees:
Pizza 1: 360/30 = 12 slices
Pizza 2: 360/45 = 8 slices
Now, the total amount made per pizza is calculated by multiplying the number of slices by the respective cost per slice:
Pizza 1: 12 * 1.95 = $23.40
Pizza 2: 8 * 2.25 = $18.00
The difference between Pizza 2 and Pizza 1 is thus represented by: 18 – 23.40 = –$5.40
Example Question #3 : Circles
What percentage of a full circle is the following sector? (Round to the nearest tenth of a percent.)
Note: The figure is not drawn to scale.
In order to find the percentage of a sector from an angle, you need to know that a full circle is 
Therefore, we can find the percentage by dividing the angle of the sector by 
Example Question #1 : Circles
A sector of a circle contains a center angle that is 36 degrees. What percentage of the circle is the sector?
Proportions can be used to determine the percentage. Let 
Cross multiply
Solve for x.
All High School Math Resources
