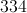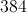We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #4 : How To Do Word Problems Where Two Quantities Are Unknown

Michael has red shirts and blue shirts, such that the ratio is red shirts for every blue shirts. What is the minimum number of shirts he can have?

Possible Answers:

There is insufficient information to answer the question.

Correct answer:

Explanation:

It really doesn't matter what and are. What matters is the ratio given to us, red: blue. Let's assume that he can only have whole shirts. That means that the minimum number of red shirts he can have is , and the minimum number of blue is , giving us a total of .

Report an Error

Example Question #4 : How To Do Word Problems Where Two Quantities Are Unknown

Two cars leave a city at the same time. One heads east at $35\: mph$ and the other heads west at $67\: mph$ . How far apart are they after hours?

Possible Answers:

$96\text{ miles}$

$201\text{ miles}$

$105\text{ miles}$

$1.9\text{ miles}$

$306\text{ miles}$

Correct answer:

$306\text{ miles}$

Explanation:

Remember, $\text{distance}={\text{rate}}*{\text{time}}$ . If we look at the car going east, this would mean:

$\text{distance}={\text{rate}}*{\text{time}}$

$\text{distance}=35\: mph*3\text{ hours}$

$\text{distance}=105\text{ miles}$

If we look at the car going west, then:

$\text{distance}={\text{rate}}*{\text{time}}$

$\text{distance}=67\: mph*3\text{ hours}$

$\text{distance}=201\text{ miles}$

Therefore, we need to add the two distances to find the total distance between them.

$T=201\text{ miles}+105 \text{ miles}$

$T=306\text{ miles}$

Report an Error

Example Question #1 : Geometry

What is the perimeter of a regular hendecagon with a side length of 32?

Possible Answers:

384

334

352

320

Correct answer:

352

Explanation:

To find the perimeter of a regular hendecagon you must first know the number of sides in a hendecagon is 11.

When you know the number of sides of a regular polygon to find the perimeter you must multiply the side length by the number of sides.

In this case it is 11*32=352 .

The answer for the perimeter is 352 .

Report an Error

Example Question #131 : High School Math

All segments of the polygon meet at right angles (90 degrees). The length of segment $\overline{AB}$ is 10. The length of segment $\overline{BC}$ is 8. The length of segment $\overline{DE}$ is 3. The length of segment $\overline{GH}$ is 2.

Find the perimeter of the polygon.

Possible Answers:

$\dpi{100} \small 46$

$\dpi{100} \small 48$

$\dpi{100} \small 42$

$\dpi{100} \small 40$

$\dpi{100} \small 44$

Correct answer:

$\dpi{100} \small 46$

Explanation:

The perimeter of the polygon is 46. Think of this polygon as a rectangle with two of its corners "flipped" inwards. This "flipping" changes the area of the rectangle, but not its perimeter; therefore, the top and bottom sides of the original rectangle would be 12 units long $\dpi{100} \small (10+2=12)$ . The left and right sides would be 11 units long $\dpi{100} \small (8+3=11)$ . Adding all four sides, we find that the perimeter of the recangle (and therefore, of this polygon) is 46.

Report an Error

Example Question #2 : How To Find The Perimeter Of A Polygon

What is the perimeter of a regular nonagon with a side length of ?

Possible Answers:

120

105

135

150

Correct answer:

135

Explanation:

To find the perimeter of a regular polygon, we take the length of each side, , and multiply it by the number of sides, .

P=s*l

In a nonagon the number of sides is , and in this example the side length is .

P=9*15=135

The perimeter is 135 .

Report an Error

Example Question #2 : Geometry

Find the perimeter of the following octagon:

Possible Answers:

$96\ m$

$56\ m$

$76\ m$

$66\ m$

$86\ m$

Correct answer:

$96\ m$

Explanation:

The formula for the perimeter of an octagon is P = 8(side) .

Plugging in our values, we get:

$P = 8(12\ m)$

$P = 96\ m$

Report an Error

Example Question #2 : Geometry

What is the area of a regular heptagon with an apothem of 4 and a side length of 6?

Possible Answers:

Correct answer:

Explanation:

What is the area of a regular heptagon with an apothem of 4 and a side length of 6?

To find the area of any polygon with the side length and the apothem we must know the equation for the area of a polygon which is

First, we must calculate the perimeter using the side length.

To find the perimeter of a regular polygon we take the length of each side and multiply it by the number of sides.

In a heptagon the number of sides is 7 and in this example the side length is 6 so

The perimeter is .

Then we plug in the numbers for the apothem and perimeter into the equation yielding

We then multiply giving us the area of .

Report an Error

Example Question #5 : Plane Geometry

What is the area of a regular decagon with an apothem of 15 and a side length of 25?

Possible Answers:

3750

2750

375

1875

Correct answer:

1875

Explanation:

To find the area of any polygon with the side length and the apothem we must know the equation for the area of a polygon which is

First, we must calculate the perimeter using the side length.

To find the perimeter of a regular polygon we take the length of each side and multiply it by the number of sides.

In a decagon the number of sides is 10 and in this example the side length is 25 so 25*10=250

The perimeter is 250 .

Then we plug in the numbers for the apothem and perimeter into the equation yielding $Area\:of\:Polygon=\frac{1}{2}(250)15$

We then multiply giving us the area of 1875 .

Report an Error

Example Question #3 : Geometry

What is the area of a regular heptagon with an apothem of and a side length of ?

Possible Answers:

112

224

Correct answer:

112

Explanation:

To find the area of any polygon with the side length and the apothem we must know the equation for the area of a polygon which is

We must then calculate the perimeter using the side length.

To find the perimeter of a regular polygon we take the length of each side and multiply it by the number of sides .

In a heptagon the number of sides is and in this example the side length is so 8*7=56

The perimeter is 56.

Then we plug in the numbers for the apothem and perimeter into the equation yielding $Area=(\frac{1}{2})(56)(4)$

We then multiply giving us the area of 112 .

Report an Error

Example Question #4 : Geometry

Find the area of the shaded region:

Screen_shot_2014-02-27_at_6.53.35_pm

Possible Answers:

75m^2

$100\pi m^2 - 25m^2$

$100m^2 + 25\pi m^2$

$100m^2 - 25\pi m^2$

$75\pi m^2$

Correct answer:

$100m^2 - 25\pi m^2$

Explanation:

To find the area of the shaded region, you must subtract the area of the circle from the area of the square.

The formula for the shaded area is:

$A=A_{square}-A_{circle}$

$A = (s)^2 - \pi(r)^2$ ,

where is the side of the square and is the radius of the circle.

Plugging in our values, we get:

$A = (10m)^2 - \pi(5m)^2$

$A = 100m^2 - 25\pi m^2$

Report an Error

View Tutors

Aaron
Certified Tutor

Austin Peay State University, Bachelor, Education.

View Tutors

Samuel
Certified Tutor

York University, Bachelor, Physics. York University, Master's/Graduate, Mathematics and Statistics.

View Tutors

Ridvan
Certified Tutor

Missouri University of Science and Technology, Bachelor of Science, Civil Engineering. University of Oklahoma Norman Campus, ...

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

MCAT Tutors in Denver, Computer Science Tutors in Houston, Computer Science Tutors in Phoenix, French Tutors in San Francisco-Bay Area, GRE Tutors in Phoenix, ACT Tutors in Chicago, Statistics Tutors in Boston, ISEE Tutors in San Diego, ACT Tutors in Washington DC, Algebra Tutors in Chicago

Popular Courses & Classes

LSAT Courses & Classes in Seattle, SSAT Courses & Classes in Miami, SSAT Courses & Classes in Los Angeles, MCAT Courses & Classes in Denver, ISEE Courses & Classes in Seattle, GRE Courses & Classes in Seattle, MCAT Courses & Classes in Washington DC, Spanish Courses & Classes in Boston, LSAT Courses & Classes in Miami, LSAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

MCAT Test Prep in Houston, SAT Test Prep in Phoenix, SAT Test Prep in Denver, ACT Test Prep in Los Angeles, LSAT Test Prep in Denver, LSAT Test Prep in Chicago, SSAT Test Prep in Miami, SAT Test Prep in Chicago, ISEE Test Prep in Seattle, ACT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #4 : How To Do Word Problems Where Two Quantities Are Unknown

Example Question #4 : How To Do Word Problems Where Two Quantities Are Unknown

Example Question #1 : Geometry

Example Question #131 : High School Math

Example Question #2 : How To Find The Perimeter Of A Polygon

Example Question #2 : Geometry

Example Question #2 : Geometry

Example Question #5 : Plane Geometry

Example Question #3 : Geometry

Example Question #4 : Geometry

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: