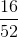We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : Number Theory

Place in order from smallest to largest:

$\frac{3}{4},\; \; \frac{1}{8},\; \; \frac{5}{8},\; \; \frac{1}{6},\; \; \frac{1}{2},\; \; \frac{1}{5},\; \; \frac{1}{3}$

Possible Answers:

$\frac{1}{8},\; \; \frac{1}{5},\; \; \frac{1}{2},\; \; \frac{3}{4},\; \; \frac{1}{6},\; \; \frac{1}{3},\; \; \frac{5}{8}$

$\frac{1}{5},\; \; \frac{3}{4},\; \; \frac{1}{3},\; \; \frac{1}{2},\; \; \frac{5}{8},\; \; \frac{1}{8},\; \; \frac{1}{6}$

$\frac{1}{2},\; \; \frac{3}{4},\; \; \frac{1}{6},\; \; \frac{5}{8},\; \; \frac{1}{3},\; \; \frac{1}{5},\; \; \frac{1}{8}$

$\frac{1}{2},\; \; \frac{1}{3},\; \; \frac{3}{4},\; \; \frac{1}{5},\; \; \frac{1}{6},\; \; \frac{1}{8},\; \; \frac{5}{8}$

$\frac{1}{8},\; \; \frac{1}{6},\; \; \frac{1}{5},\; \; \frac{1}{3},\; \; \frac{1}{2},\; \; \frac{5}{8},\; \; \frac{3}{4}$

Correct answer:

$\frac{1}{8},\; \; \frac{1}{6},\; \; \frac{1}{5},\; \; \frac{1}{3},\; \; \frac{1}{2},\; \; \frac{5}{8},\; \; \frac{3}{4}$

Explanation:

To place in order, first we must find a common denominator and convert all fractions to that denominator.

$2, \;4,\; 8$ have a common denominator of .

$6,\; 3$ have a common denominator of .

6, 8, 5 have a common denominator of 120 .

Therefore we can use common denominators to make all of the fractions look similar. Then the ordering becomes trivial.

$\frac{1}{8}=\frac{15}{120},\; \; \frac{1}{6}=\frac{20}{120},\; \; \frac{1}{5}=\frac{24}{120}$

$\frac{1}{3}=\frac{40}{120},\; \; \frac{1}{2}=\frac{60}{120}$

$\frac{5}{8}=\frac{75}{120},\; \; \frac{3}{4}=\frac{90}{120}$

Report an Error

Example Question #3 : Number Theory

What number is $20\%$ of ?

Possible Answers:

Correct answer:

Explanation:

For percent problems there are verbal cues:

"IS" means equals and "OF" means multiplication.

Then the equation to solve becomes:

$n=0.20\cdot 15=3$

Report an Error

Example Question #4 : Number Theory

Which of the following is NOT a real number?

Possible Answers:

$\sqrt{-9}$

$\sqrt{84}$

$4i^{2}$

$4\pi$

Correct answer:

$\sqrt{-9}$

Explanation:

We are looking for a number that is not real.

$4\pi$ , , and $\sqrt{84}$ are irrational numbers, but they are still real.

Then, $4i^{2}$ is equivalent to by the rules of complex numbers. Thus, it is also real.

That leaves us with: $\sqrt{-9}$ which in fact is imaginary (since no real number multiplied by itself yields a negative number) and simplifies to .

Report an Error

Example Question #1 : Algebra Ii

Which of the following are considered real numbers?

Possible Answers:

1.9344

$\frac{3}{2}$

$\pi$

$\textup{All of the above}$

Correct answer:

$\textup{All of the above}$

Explanation:

Real numbers can be found anywhere on a continuous number line ranging from negative infinity to positive infinity; therefore, all of the numbers are real numbers.

Report an Error

Example Question #2 : Algebra Ii

If a card is drawn randomly from a regular shuffled 52 card deck, what is the probability that the card is either a spade or a 3?

Possible Answers:

$\frac{7}{52}$

$\frac{5}{52}$

$\frac{2}{13}$

$\frac{4}{13}$

$\frac{17}{52}$

Correct answer:

$\frac{4}{13}$

Explanation:

How many cards in the deck are either a spade or a 3?

There are thirteen spades, including a 3 of spades.

There are four 3's, including a 3 of spades.

Since we are counting the same card (3 of spades) twice, there are actually

13+4-1

=16 distinct cards that fit the criteria of being either a spade or a 3.

Since any of the 52 cards is equally likely to be drawn, the probability that it is a spade or a 3, is

$\frac{16}{52}$ $=\frac{4}{13}$

Report an Error

Example Question #5 : Number Theory

Find the distance between and on a number line.

Possible Answers:

7.5

10.25

Correct answer:

Explanation:

To find the distance on a number line:

$d=x_{2}-x{{_1}}$

d=11-(-4)

d=11+4

d=15

Report an Error

Example Question #1 : How To Find The Perimeter Of A Hexagon

What is the perimeter of a regular hexagon with a side length of 12?

Possible Answers:

Correct answer:

Explanation:

To find the perimeter of a regular hexagon you must first know the number of sides in a hexagon which is 6.

When you know the number of sides of a regular polygon to find the perimeter you must multiply the side length by the number of sides.

In this case it is 6*12=72

The answer for the perimeter is .

Report an Error

Example Question #1 : Hexagons

How many degrees is the interior angle of any regular hexagon?

Possible Answers:

120^o

160^o

90^o

60^o

Correct answer:

120^o

Explanation:

$interior\ angle=\frac{(n-2)*180^o}{n}$

To find the angle of any regular polygon, you find the number of sides, . In this example n=6 .

$interior\ angle=\frac{(n-2)*180^o}{n}=\frac{(6-2)*180^o}{6}$

You then subtract from the number of sides, yielding .

Take and multiply it by 180^o to yield the total number of degrees in the regular hexagon.

(n-2)*180^o=4*180^o=720^o

Then, to find one individual angle, we divide 720^o by the total number of angles, .

$\frac{720^o}{6}=120^o$

The answer is 120^o .

Report an Error

Example Question #1 : How To Find The Perimeter Of A Hexagon

What is the perimeter of a hexagon with a side length of ?

Possible Answers:

Correct answer:

Explanation:

To find the perimeter of a regular polygon, we take the length of each side, , and multiply it by the number of sides, .

P=s*l

In a hexagon the number of sides is , and in this example the side length is .

P=6*4=24

The perimeter is .

Report an Error

Example Question #1 : How To Find The Perimeter Of A Hexagon

How many lines of symmetry can be found in a regular hexagon?

Possible Answers:

$\infty$

Correct answer:

Explanation:

The number of lines of symmetry through a regular polygon is equal to the number of sides.

A hexagon has lines of symmetry through each vertex, giving three lines of symmetry that each connect two opposite vertices. The other three lines pass through the midpoints of opposite sides of the hexagon.

Report an Error

View Tutors

Shweta
Certified Tutor

Virginia Commonwealth University, Bachelor of Science, Biology, General.

View Tutors

Ahlem
Certified Tutor

University of Tunis I, Bachelors, Arabic Studies and Civilisation. University of South Florida-Main Campus, Masters, French a...

View Tutors

Luz Stephanie
Certified Tutor

Benemerita Universidad Autónoma de Puebla, Bachelor of Science, Physics.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in San Francisco-Bay Area, Chemistry Tutors in Phoenix, Calculus Tutors in Denver, Algebra Tutors in Boston, GMAT Tutors in Seattle, Statistics Tutors in Atlanta, Math Tutors in Boston, LSAT Tutors in Boston, LSAT Tutors in New York City, Computer Science Tutors in Seattle

Popular Courses & Classes

SAT Courses & Classes in Chicago, ISEE Courses & Classes in Boston, ISEE Courses & Classes in Washington DC, LSAT Courses & Classes in Philadelphia, SSAT Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Atlanta, ACT Courses & Classes in Miami, MCAT Courses & Classes in Chicago, ACT Courses & Classes in San Diego, GRE Courses & Classes in Phoenix

Popular Test Prep

GRE Test Prep in Phoenix, LSAT Test Prep in Philadelphia, ACT Test Prep in Houston, SSAT Test Prep in Denver, ISEE Test Prep in Seattle, MCAT Test Prep in Atlanta, SSAT Test Prep in Seattle, SAT Test Prep in Chicago, ACT Test Prep in Chicago, ACT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #2 : Number Theory

Example Question #3 : Number Theory

Example Question #4 : Number Theory

Example Question #1 : Algebra Ii

Example Question #2 : Algebra Ii

Example Question #5 : Number Theory

Example Question #1 : How To Find The Perimeter Of A Hexagon

Example Question #1 : Hexagons

Example Question #1 : How To Find The Perimeter Of A Hexagon

Example Question #1 : How To Find The Perimeter Of A Hexagon

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: