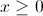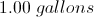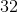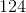Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Algebra II

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : Inequalities

Solve the inequality for x:

2x+4>64 $\displaystyle 2x+4>64$

Possible Answers:

x>30 $\displaystyle x>30$

x>28 $\displaystyle x>28$

x<28 $\displaystyle x< 28$

x<30 $\displaystyle x< 30$

x=30 $\displaystyle x=30$

Correct answer:

x>30 $\displaystyle x>30$

Explanation:

2x+4>64 $\displaystyle 2x+4>64$

Subtract 4 from both sides:

2x > 60 $\displaystyle 2x > 60$

Divide both sides by 2:

x > 30 $\displaystyle x > 30$

Report an Error

Example Question #1 : Solving Inequalities

Solve for $\displaystyle x$.

$-7x-4\geq10$ $\displaystyle -7x-4\geq10$

Possible Answers:

$x\leq2$ $\displaystyle x\leq2$

$x\geq-2$ $\displaystyle x\geq-2$

$x\geq2$ $\displaystyle x\geq2$

$x\leq-2$ $\displaystyle x\leq-2$

Correct answer:

$x\leq-2$ $\displaystyle x\leq-2$

Explanation:

$-7x-4\geq10$ $\displaystyle -7x-4\geq10$

Add 4 to both sides.

$-7x\geq14$ $\displaystyle -7x\geq14$

Divide both sides by –7. When dividing by a negative value, we must also change the direction of the inequality sign.

$x\leq-2$ $\displaystyle x\leq-2$

Report an Error

Example Question #4 : Inequalities

Solve for $\displaystyle x$:

$9x-27\geq6x$ $\displaystyle 9x-27\geq6x$

Possible Answers:

$x\geq3$ $\displaystyle x\geq3$

$x\geq9$ $\displaystyle x\geq9$

$x\leq3$ $\displaystyle x\leq3$

$x\leq9$ $\displaystyle x\leq9$

x>9 $\displaystyle x>9$

Correct answer:

$x\geq9$ $\displaystyle x\geq9$

Explanation:

$9x-27\geq6x$ $\displaystyle 9x-27\geq6x$

Move like terms to the same sides:

$9x-6x\geq27$ $\displaystyle 9x-6x\geq27$

Combine like terms:

$3x\geq27$ $\displaystyle 3x\geq27$

Divide both sides by 3:

$x\geq9$ $\displaystyle x\geq9$

Report an Error

Example Question #241 : Algebra Ii

Solve for $\displaystyle x$:

$5-3x\leq14$ $\displaystyle 5-3x\leq14$

Possible Answers:

$x\leq3$ $\displaystyle x\leq3$

$x\geq3$ $\displaystyle x\geq3$

$x\geq0$ $\displaystyle x\geq0$

$x\geq9$ $\displaystyle x\geq9$

$x\geq-3$ $\displaystyle x\geq-3$

Correct answer:

$x\geq-3$ $\displaystyle x\geq-3$

Explanation:

Inequalities can be treated like any other equation except when multiplying and dividing by negative numbers. When multiplying or dividing by negative numbers, we just flip the sign of the inequality so that $\displaystyle >$ becomes $\displaystyle < $, and vice versa.

$5-3x\leq14$ $\displaystyle 5-3x\leq14$

$-3x\leq9$ $\displaystyle -3x\leq9$

$\frac{-3x}{-3}\geq\frac{9}{-3}$ $\displaystyle \frac{-3x}{-3}\geq\frac{9}{-3}$

$x\geq-3$ $\displaystyle x\geq-3$

Report an Error

Example Question #242 : Algebra Ii

Sarah notices her map has a scale of $\frac{1}{4}\; in=1\; mile$ $\displaystyle \frac{1}{4}\; in=1\; mile$. She measures $12.5\; in$ $\displaystyle 12.5\; in$ between Beaver Falls and Chipmonk Cove. How far apart are the cities?

Possible Answers:

$90\; miles$ $\displaystyle 90\; miles$

$25\; miles$ $\displaystyle 25\; miles$

$50\; miles$ $\displaystyle 50\; miles$

$75\; miles$ $\displaystyle 75\; miles$

$60\; miles$ $\displaystyle 60\; miles$

Correct answer:

$50\; miles$ $\displaystyle 50\; miles$

Explanation:

$\frac{1}{4}\; in=1\; mile$ $\displaystyle \frac{1}{4}\; in=1\; mile$ is the same as $1\; in = 4\; miles$ $\displaystyle 1\; in = 4\; miles$

So to find out the distance between the cities

$12.5\; in \cdot \frac{4\; miles}{1\;in }=50\; miles$ $\displaystyle 12.5\; in \cdot \frac{4\; miles}{1\;in }=50\; miles$

Report an Error

Example Question #243 : Algebra Ii

Sunshine paint is made by mixing three parts yellow paint and one part red paint. How many gallons of yellow paint should be mixed with two quarts of red paint?

(1 gallon = 4 quarts)

Possible Answers:

$0.75\; gallons$ $\displaystyle 0.75\; gallons$

$1.50\; gallons$ $\displaystyle 1.50\; gallons$

$1.75\; gallons$ $\displaystyle 1.75\; gallons$

$1.00\; gallons$ $\displaystyle 1.00\; gallons$

$0.50\; gallons$ $\displaystyle 0.50\; gallons$

Correct answer:

$1.50\; gallons$ $\displaystyle 1.50\; gallons$

Explanation:

First set up the proportion:

$\frac{3\; parts \; yellow}{1 \; part\; red}=\frac{x \; quarts \; yellow}{2 \; quarts \; red}$ $\displaystyle \frac{3\; parts \; yellow}{1 \; part\; red}=\frac{x \; quarts \; yellow}{2 \; quarts \; red}$

x = $6 \; quarts\;yellow\; paint$ $\displaystyle 6 \; quarts\;yellow\; paint$

Then convert this to gallons:

$6 \; quarts\; \cdot \frac{1 \; gallon}{4\; quarts}= 1.50\; gallons$ $\displaystyle 6 \; quarts\; \cdot \frac{1 \; gallon}{4\; quarts}= 1.50\; gallons$

Report an Error

Example Question #246 : Algebra Ii

If $\displaystyle y$ is directly proportional to $\displaystyle x$, and x=2 $\displaystyle x=2$ when y=8 $\displaystyle y=8$, find a formula for $\displaystyle y$.

Possible Answers:

y=8x $\displaystyle y=8x$

$y=\frac{x}{4}$ $\displaystyle y=\frac{x}{4}$

y=4x $\displaystyle y=4x$

$\frac{y}{4}=x$ $\displaystyle \frac{y}{4}=x$

y=2x $\displaystyle y=2x$

Correct answer:

y=4x $\displaystyle y=4x$

Explanation:

8=k*2 $\displaystyle 8=k*2$ since x=2 $\displaystyle x=2$ and y=8 $\displaystyle y=8$

Solving for $\displaystyle k$, you get that k=4 $\displaystyle k=4$

Replacing $\displaystyle k$ in the original equation, you get the answer of

y=4x $\displaystyle y=4x$

Report an Error

Example Question #244 : Algebra Ii

If $\displaystyle y$ is inversely proportional to $\displaystyle x$, and if x=2 $\displaystyle x=2$ when y=8 $\displaystyle y=8$, find a formula for $\displaystyle y$.

Possible Answers:

$y=\frac{16}{x}$ $\displaystyle y=\frac{16}{x}$

y=4x $\displaystyle y=4x$

$y=\frac{x}{16}$ $\displaystyle y=\frac{x}{16}$

$\frac{16}{y}=x$ $\displaystyle \frac{16}{y}=x$

y=16x $\displaystyle y=16x$

Correct answer:

$y=\frac{16}{x}$ $\displaystyle y=\frac{16}{x}$

Explanation:

Since y is inversely porportional to x, you can use the standard equations of $y=\frac{k}{x}$ $\displaystyle y=\frac{k}{x}$ where k is a constant. Plugging the given x and y into this equation to solve for k, k=16 $\displaystyle k=16$. To get the answer, substitute k into the standard equation.

Report an Error

Example Question #241 : Algebra Ii

If $f(x)=x^{3}-1$ $\displaystyle f(x)=x^{3}-1$ and $g(x)=x^{2}+1$ $\displaystyle g(x)=x^{2}+1$, what is g(f(2)) $\displaystyle g(f(2))$?

Possible Answers:

124 $\displaystyle 124$

$\displaystyle 12$

$\displaystyle 50$

$\displaystyle 90$

$\displaystyle 32$

Correct answer:

$\displaystyle 50$

Explanation:

g(f(2)) $\displaystyle g(f(2))$ is a composite function where f(2) $\displaystyle f(2)$ is plugged into g(x) $\displaystyle g(x)$:

$f(2)=(2)^{3}-1=8-1=7$ $\displaystyle f(2)=(2)^{3}-1=8-1=7$

$g(7)=(7)^{2}+1=49+1=50$ $\displaystyle g(7)=(7)^{2}+1=49+1=50$

Report an Error

Example Question #1 : Simplifying Polynomials

Simplify the following expression:

$3x^9y^4 \cdot (2y)^3$ $\displaystyle 3x^9y^4 \cdot (2y)^3$.

Possible Answers:

$24x^9y^{12}$ $\displaystyle 24x^9y^{12}$

$\displaystyle 11x^9y^7$

$\displaystyle 24x^9y^7$

$\displaystyle 18x^9y^6$

Correct answer:

$\displaystyle 24x^9y^7$

Explanation:

First, multiply out the second expression so that you get 8y^3 $\displaystyle 8y^3$.

Then, multiply your like terms, taking care to remember that when multiplying terms that have the same base, you add the exponents. Thus, you get $24x^9y^{12}$ $\displaystyle 24x^9y^{12}$.

Report an Error

View Tutors

Candice
Certified Tutor

University of Memphis, Bachelor of Education, Education. Strayer University-Tennessee, Masters in Education, Educational, Ins...

View Tutors

Heather
Certified Tutor

Western Governors University, Bachelor of Education, Special Education.

View Tutors

Keri
Certified Tutor

California State University-Chico, Bachelor in Arts, Communication, General. University of Southern Maine, Master of Arts, Am...

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Calculus Tutors in Philadelphia, Biology Tutors in Miami, Biology Tutors in New York City, GMAT Tutors in San Francisco-Bay Area, ISEE Tutors in Denver, Biology Tutors in Los Angeles, SSAT Tutors in Dallas Fort Worth, GMAT Tutors in Chicago, Algebra Tutors in Denver, Algebra Tutors in New York City

Popular Courses & Classes

MCAT Courses & Classes in Houston, SSAT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Houston, MCAT Courses & Classes in Washington DC, GMAT Courses & Classes in Boston, SSAT Courses & Classes in Boston, ISEE Courses & Classes in Seattle, MCAT Courses & Classes in San Diego, GMAT Courses & Classes in Atlanta

Popular Test Prep

GMAT Test Prep in Phoenix, GMAT Test Prep in Atlanta, GRE Test Prep in Philadelphia, GMAT Test Prep in Los Angeles, GRE Test Prep in Houston, SAT Test Prep in Boston, ACT Test Prep in San Diego, LSAT Test Prep in Denver, ACT Test Prep in Washington DC, MCAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Algebra II

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #2 : Inequalities

Example Question #1 : Solving Inequalities

Example Question #4 : Inequalities

Example Question #241 : Algebra Ii

Example Question #242 : Algebra Ii

Example Question #243 : Algebra Ii

Example Question #246 : Algebra Ii

Example Question #244 : Algebra Ii

Example Question #241 : Algebra Ii

Example Question #1 : Simplifying Polynomials

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: