Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Algebra I

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Equation Of A Parallel Line

What line is parallel to 5x + 10y=7 through the point (-6,7) ?

Possible Answers:

$y=\frac{1}{3}x+5$

y=2x+19

$y=-\frac{1}{2}x+4$

$y=\frac{2}{3}x - 1$

y=3x-12

Correct answer:

$y=-\frac{1}{2}x+4$

Explanation:

The given line can be rewritten as $y=-\frac{1}{2}x+\frac{7}{10}$ , which has slope $m=-\frac{1}{2}$ .

If the new line is parallel to the old line, it must have the same slope. So we use the point-slope form of an equation to calculate the new intercept.

y=mx+b becomes $7=-\frac{1}{2}(-6)+b$ where b=4 .

So the equation of the parallel line is $y=-\frac{1}{2}x+4$ .

Report an Error

Example Question #1 : How To Find The Equation Of A Parallel Line

Find the equation of a line parallel to y=12x-5 .

Possible Answers:

$y=\frac{1}{12}x-5$

y=.12x+2

$y=-\frac{1}{12}x-5$

y=12x+2

Correct answer:

y=12x+2

Explanation:

Since parallel lines share the same slope, the only answer that works is y=12x+2.

Report an Error

Example Question #3 : How To Find The Equation Of A Parallel Line

Given the equation y=2x-13 and the point (-2,4) , find a line through the point that is parallel to the given line.

Possible Answers:

$y=\frac{1}{2}x+4$

y=2x+8

y=2x-8

$y=\frac{1}{2}x+8$

y=2x+4

Correct answer:

y=2x+8

Explanation:

In order for two lines to be parallel, they must have the same slope. The slope of the given line is , so we know that the line going through the given point also has to have a slope of . Using the point-slope formula,

$y-y_{1}=m(x-x_1)$ ,

where represents the slope and y_1 and x_1 represent the given points, plug in the points given and simplify into standard form:

y-4=2(x-(-2))

y-4=2x+4

y=2x+8

Report an Error

Example Question #64 : Algebra I

What line is parallel to y=2x+1 through (3,-9) ?

Possible Answers:

$y=\frac{1}{2}x-10$

y=-2x+3

y=2x-15

y=3x-9

$y=\frac{-1}{2}x+5$

Correct answer:

y=2x-15

Explanation:

Parallel lines have the same slopes. The slope for the given equation is . We can use the slope and the new point in the slope intercept equation to solve for the intercept:

y=mx+b

-9=2(3)+b

b=-15

Therefore the new equation becomes:

y=2x-15

Report an Error

Example Question #4 : How To Find The Equation Of A Parallel Line

What line is parallel to $y=\frac{1}{2}x-2$ through (6,7) ?

Possible Answers:

3x-2y=4

3x+5y=8

2x+3y=5

-x+2y=8

x-2y=6

Correct answer:

-x+2y=8

Explanation:

Parallel lines have the same slope. The slope of the given line is $\frac{1}{2}$ .

Find the line with slope $\frac{1}{2}$ through the point (6,7) by plugging this informatuon into the slope intercept equation, y=mx+b :

$7=\frac{1}{2}(6)+b$ , which gives 7=3+b .

Solve for by subtracting from both sides to get b=4 .

Then the parallel line equation becomes $y=\frac{1}{2}x+4$ , and converting to standard form gives -x+2y=8 .

Report an Error

Example Question #2 : How To Find The Equation Of A Parallel Line

Find the equation of a line parallel to the line that goes through points $\left ( 2,4 \right )$ and $\left ( 0,7 \right )$ .

Possible Answers:

y=3x+4

$y=\frac{2}{3}X+7$

$y=\frac{3}{2}X-5$

$y=-\frac{3}{2}X+7$

Correct answer:

$y=-\frac{3}{2}X+7$

Explanation:

Parallel lines share the same slope. Because the slope of the original line is $-\frac{3}{2}$ , the correct answer must have that slope, so the correct answer is

$y=-\frac{3}{2}X+7$

Report an Error

Example Question #1 : Graphing

The vertices of a triangle are given by $(0,3), \; (0,5),\; and \; (-2,4)$ . The triangle is rotated about the origin by degrees clockwise. What are the new coordinates?

Possible Answers:

$(6,0), \; (10,0),\; and \; (8,4)$

$(4,1), \; (6,1),\; and \; (5,3)$

$(-9,0), \; (-15,0),\; and \; (-12,-6)$

$(-3,0), \; (-5,0),\; and \; (-4,-2)$

$(3,0), \; (5,0),\; and \; (4,2)$

Correct answer:

$(3,0), \; (5,0),\; and \; (4,2)$

Explanation:

The coordinates form a triangle in the second quadrant with a side along the y-axis. The rotation about the origin by degrees clockwise results in a triangle in the first quadrant with a side along the x-axis. There are two responses that give triangles along the x-axis:

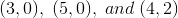
$(3,0), \; (5,0),\; and \; (4,2)$ and

$(6,0), \; (10,0),\; and \; (8,4)$

A rotation and a dialation by a factor of is given by

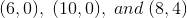
$(6,0), \; (10,0),\; and \; (8,4)$ , so the correct answer is $(3,0), \; (5,0),\; and \; (4,2)$

Report an Error

Example Question #61 : Algebra I

What is the y-intercept of the equation?

y=5x+5

Possible Answers:

(0,1)

(0,0)

(0,5)

$(0,\frac{1}{5})$

(0,25)

Correct answer:

(0,5)

Explanation:

To find the y-intercept, we set the value equal to zero and solve for the value of .

y=5x+5

y=5(0)+5

y=0+5

y=5

Since the y-intercept is a point, we want to write our answer in point notation: (0,5) .

Report an Error

Example Question #2 : How To Find X Or Y Intercept

What is the x-intercept of the equation?

$y=\frac{2}{3}x+ 12$

Possible Answers:

(-18,0

(6,0)

(-12,0)

$(\frac{2}{3},0)$

(0,0)

Correct answer:

(-18,0

Explanation:

To find the x-intercept of an equation, set the value equal to zero and solve for .

$y=\frac{2}{3}x+ 12$

$0 =\frac{2}{3}x+12$

Subtract from both sides.

$0 -12 = \frac{2}{3}x +12 - 12$

$-12 = \frac{2}{3} x$

Multiply both sides by $\frac{3}{2}$ .

$(\frac{3}{2})(-12) = (\frac{2}{3} x)(\frac{3}{2})$

-18= x

Since the x-intercept is a point, we will want to write it in point notation: (-18,0

Report an Error

Example Question #3 : How To Find X Or Y Intercept

What is the y-intercept of y=5x+20?

Possible Answers:

$\frac{1}{4}$

100

Correct answer:

Explanation:

To solve for the y-intercept, set the x value equal to zero:

y=5x+20

y=5(0)+20

y=20

Report an Error

View Tutors

Joy
Certified Tutor

Boston University, Bachelor in Arts, Conservation Biology.

View Tutors

Yongmao
Certified Tutor

Nankai University, Bachelor of Science, Chemistry. Washington University in St Louis, Doctor of Philosophy, Organic Chemistry.

View Tutors

Austin
Certified Tutor

University of Arizona, Bachelor of Science, Physiology.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in Houston, GRE Tutors in San Diego, English Tutors in Boston, Math Tutors in Dallas Fort Worth, SAT Tutors in San Diego, LSAT Tutors in Boston, SAT Tutors in Chicago, Math Tutors in Miami, Algebra Tutors in Phoenix, ISEE Tutors in Boston

Popular Courses & Classes

LSAT Courses & Classes in Chicago, SAT Courses & Classes in Philadelphia, SAT Courses & Classes in New York City, SAT Courses & Classes in Chicago, Spanish Courses & Classes in Los Angeles, ACT Courses & Classes in San Diego, MCAT Courses & Classes in Denver, ISEE Courses & Classes in Seattle, GRE Courses & Classes in Chicago, ACT Courses & Classes in Atlanta

Popular Test Prep

ISEE Test Prep in Washington DC, GMAT Test Prep in Los Angeles, SSAT Test Prep in Atlanta, SSAT Test Prep in Chicago, ISEE Test Prep in Phoenix, GRE Test Prep in San Francisco-Bay Area, SAT Test Prep in Atlanta, LSAT Test Prep in Chicago, LSAT Test Prep in San Diego, ISEE Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Algebra I

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : How To Find The Equation Of A Parallel Line

Example Question #1 : How To Find The Equation Of A Parallel Line

Example Question #3 : How To Find The Equation Of A Parallel Line

Example Question #64 : Algebra I

Example Question #4 : How To Find The Equation Of A Parallel Line

Example Question #2 : How To Find The Equation Of A Parallel Line

Example Question #1 : Graphing

Example Question #61 : Algebra I

Example Question #2 : How To Find X Or Y Intercept

Example Question #3 : How To Find X Or Y Intercept

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: