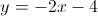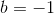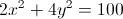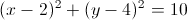Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Algebra I

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #91 : Algebra I

A straight line passes through the points (1,3) and (2,2) .

What is the -intercept of this line?

Possible Answers:

(4,0)

(3,1)

(5,0)

(0,4)

(0,5)

Correct answer:

(4,0)

Explanation:

First calculate the slope:

$(\text{change in Y})/(\text{change in x}) = (1-2)/(3-2) = -1$

The standard equation for a line is Y=a*X + b .

In this equation, is the slope of the line, and is the -intercept. All points on the line must fit this equation. Plug in either point (1,3) or (2,2).

Plugging in (1,3) we get 3=-1*1 + b .

Therefore, b = 3 - (-1) =4 .

Our equation for the line is now:

Y= (-1)X + 4

To find the -intercept, we plug in y=0 :

0=(-1)x+4

x=4

Thus, the -intercept the point (4,0).

Report an Error

Example Question #92 : Algebra I

Calculate the y-intercept of the line depicted by the equation below.

3x+6y=15

Possible Answers:

(0,5)

(0,2.5)

(5,0)

(2.5,0)

(0,6)

Correct answer:

(0,2.5)

Explanation:

To find the y-intercept, let equal 0.

3(0)+6y=15

We can then solve for the value of .

6y=15

$y=\frac{15}{6}=2.5$

The y-intercept will be (0,2.5) .

Report an Error

Example Question #25 : How To Find X Or Y Intercept

What is the x-intercept of 2y=3x+5 ?

Possible Answers:

$\frac{6}{5}$

$\frac{3}{5}$

$-\frac{5}{3}$

$-\frac{3}{5}$

$-\frac{10}{3}$

Correct answer:

$-\frac{5}{3}$

Explanation:

To find the x-intercept, set y equal to zero and solve:

2y=3x+5

2(0)=3x+5

0=3x+5

Subtract from both sides:

-5=3x

Divide both sides by to isolate x:

$\frac{-5}{3}=x$

Report an Error

Example Question #93 : Algebra I

What is the y-intercept of the equation?

$y=\frac{2}{3}x+ 12$

Possible Answers:

(0,4)

(0,12)

(0,3)

(0,0)

(0,8)

Correct answer:

(0,12)

Explanation:

$y=\frac{2}{3}x+ 12$

To find the y-intercept, we set the value equal to zero and solve for the $\small y$ value.

$y= \frac{2}{3} (0) +12$

y=12

Since the y-intercept is a point, we will need to convert our answer to point notation.

(0,12)

Report an Error

Example Question #1 : How To Find The Equation Of A Curve

What line goes through points (-3,-7) and (2,3) ?

Possible Answers:

$y=\frac{1}{2}x-3$

y=-2x-4

y=2x-1

y=2x+5

$y=\frac{-1}{2}x+3$

Correct answer:

y=2x-1

Explanation:

First, we find the slope between the two points:

$P_{1}=(-3,-7)$ and $P_{2}=(2,3)$

$m= \frac{y_{2} - y_{1}}{x_{2}-x_{1}}=\frac{3-(-7)}{2-(-3)}=\frac{10}{5}=2$

Plug the slope and one point into the slope-intercept form to calculate the intercept:

y=mx+b

3=2(2)+b

b=-1

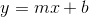
Thus the equation between the points becomes y=2x-1 .

Report an Error

Example Question #1 : How To Find The Equation Of A Circle

The center of a circle is (2, 4) and its radius is . Which of the following could be the equation of the circle?

Possible Answers:

$(x - 2)^{2} + (y - 4)^{2} = 100$

$(x + 2)^{2} + (y + 4)^{2} = 100$

$2x^{2} + 4y^{2} = 100$

$x^{2} + y^{2} = 100$

$(x - 2)^{2} + (y - 4)^{2} = 10$

Correct answer:

$(x - 2)^{2} + (y - 4)^{2} = 100$

Explanation:

The general equation of a circle is $(x - h)^{2} + (y - k)^{2} = r^{2}$ , where the center of the circle is (h, k) and the radius is .

Thus, we plug the values given into the above equation to get $(x - 2)^{2} + (y - 4)^{2} = 100$ .

Report an Error

Example Question #2 : How To Find The Equation Of A Circle

Which one of these equations accurately describes a circle with a center of (2,3) and a radius of ?

Possible Answers:

(x-3)^2+(y-2)^2=25

x^2+y^2=25

(x-2)^2+(y-3)^2-25=0

(x^2+4)-(y^2+9)=25

$\sqrt{x^2+y^2-3^2-2^2}=5$

Correct answer:

(x-2)^2+(y-3)^2-25=0

Explanation:

The standard formula for a circle is (x-a)^2+(y-b)^2=r^2 , with (a,b) the center of the circle and the radius.

Plug in our given information.

(x-a)^2+(y-b^2)=r^2

(x-2)^2+(y-3)^2=25

This describes what we are looking for. This equation is not one of the answer choices, however, so subtract from both sides.

(x-2)^2+(y-3)^2-25=0

Report an Error

View Tutors

Maya
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Animation and Special Effects.

View Tutors

Alex
Certified Tutor

Vanderbilt University, Bachelor of Science, Psychology. Boston University, Master of Science, Speech-Language Pathology.

View Tutors

Michelle
Certified Tutor

University of Rhode Island, Bachelor of Science, Marine Biology. University of Rhode Island, Master of Arts, High School Teac...

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in Denver, Computer Science Tutors in Philadelphia, SSAT Tutors in Chicago, SAT Tutors in San Diego, Statistics Tutors in Philadelphia, Calculus Tutors in Los Angeles, Computer Science Tutors in Boston, Math Tutors in Phoenix, GRE Tutors in Los Angeles, French Tutors in San Diego

Popular Courses & Classes

GRE Courses & Classes in San Diego, MCAT Courses & Classes in New York City, GMAT Courses & Classes in Dallas Fort Worth, ACT Courses & Classes in San Diego, GMAT Courses & Classes in Miami, ACT Courses & Classes in New York City, SAT Courses & Classes in Philadelphia, GMAT Courses & Classes in San Diego, ISEE Courses & Classes in Boston, Spanish Courses & Classes in San Francisco-Bay Area

Popular Test Prep

MCAT Test Prep in Philadelphia, MCAT Test Prep in San Francisco-Bay Area, ISEE Test Prep in Boston, ISEE Test Prep in Seattle, GRE Test Prep in Seattle, SSAT Test Prep in Washington DC, SSAT Test Prep in Los Angeles, ACT Test Prep in New York City, LSAT Test Prep in San Diego, SSAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Algebra I

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #91 : Algebra I

Example Question #92 : Algebra I

Example Question #25 : How To Find X Or Y Intercept

Example Question #93 : Algebra I

Example Question #1 : How To Find The Equation Of A Curve

Example Question #1 : How To Find The Equation Of A Circle

Example Question #2 : How To Find The Equation Of A Circle

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: