All GRE Subject Test: Math Resources
Example Questions
Example Question #13 : Conic Sections
Find the intersection(s) of the two parabolas: 

Set both parabolas equal to each other and solve for x.
Substitute both values of 

The coordinates of intersection are:

Example Question #4 : Solve A System Of Quadratic Equations
Find the points of intersection:

To solve, set both equations equal to each other:
To solve as a quadratic, combine like terms by adding/subtracting all three terms from the right side to the left side:
This simplifies to
Solving by factoring or the quadratic formula gives the solutions 

Plugging each into either original equation gives us:
Our coordinate pairs are 

Example Question #71 : Calculus
Evaluate:
Evaluating this integral requires use of the "Product to Sum Formulas of Trigonometry":
For:
So for our given integral, we can rewrite like so:
This can be rewritten as two separate integrals and solved using a simple substitution.
Solving each integral individually, we have:
Substituting this into the integral results in:
The other integral is solved the same way:
Substituting this into the integral results in:
Now combining these two statements together results in one of the answer choices:
Example Question #1 : Integrals
Evaluate:
This integral can be easily evaluated by following the rules outlined for integrating powers of sine and cosine.
But first a substitution needs to be made:
Now that we've made this substitution, we will use the rules outlined for integrating powers of sine and cosine:
In General:
1. If "m" is odd, then we make the substitution 

2. If "n" is odd, then we make the substitution 

For our given problem statement we will use the first rule, and alter the integral like so:
Now we need to substitute back into v:
Now we need to substitute back into u, and rearrange to make it look like one of the answer choices:
Example Question #1 : Sine
Find 
Step 1: Draw a 
The short sides have a length of 

Step 2: Find Sin (Angle A):
Step 3: Rationalize the root at the bottom:
Example Question #71 : Functions And Graphs
Evaluate the derivative
1
The inverse trig functions should be memorized.
The other common inverse trig functions are
Example Question #1 : Limits
Evaluate:
Undefined/No Limit
Step 1: See if we can plug in 
We can't because the denominator becomes 
Step 2: Factor the denominator:
Step 3: Re-write the function:
Step 4: Divide by 
We are left with:
Step 5: Plug in 
The limit of this function as x approaches 2 is 
Example Question #72 : Calculus
Evaluate:
The limit does not exist.
Let's examine the limit
first.
and

so by L'Hospital's Rule,
Since 
Now, for each 

By the Squeeze Theorem,
and
Example Question #1 : L'hospital's Rule
Evaluate:
The limit does not exist.
Therefore, by L'Hospital's Rule, we can find 
Similarly,
So
But 

Example Question #12 : New Concepts
Evaluate:
The limit does not exist.
and
Therefore, by L'Hospital's Rule, we can find 
Similarly,
so
All GRE Subject Test: Math Resources






























![\sin(\alpha x)\cos(\beta x)=\frac{1}{2}[\sin((\alpha - \beta)x)+\sin((\alpha + \beta)x)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/426371/gif.latex)
![\int \sin(75x)\cos(52x)dx\rightarrow \frac{1}{2}\int[\sin(23x)+\sin(127x)]dx](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/426372/gif.latex)
![\frac{1}{2}\int[\sin(23x)+\sin(127x)]dx\rightarrow \frac{1}{2}\int \sin(23x)dx+\frac{1}{2}\int\sin(127x)dx](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/426373/gif.latex)


















![\frac{1}{2}\int\sin^4(u)[\cos^2(u)]^2\cos(u)du\rightarrow\frac{1}{2}\int\sin^4(u)[1-\sin^2(u)]^2\cos(u)du](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/430221/gif.latex)

![\frac{1}{2}\int v^4[1-v^2]^2dv\rightarrow\frac{1}{2}\int v^4[1-2v^2+v^4]dv\rightarrow\frac{1}{2}\int (v^4-2v^6+v^8)dv](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/430223/gif.latex)
![\frac{1}{2}[\frac{1}{5}v^5-\frac{2}{7}v^7+\frac{1}{9}v^9]+C\rightarrow\frac{1}{10}v^5-\frac{1}{7}v^7+\frac{1}{18}v^9+C](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/430224/gif.latex)












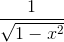
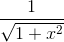








![\frac {(x-2)}{[(x-2)(x+2)]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/725550/gif.latex)