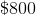GRE Math : GRE Quantitative Reasoning

Study concepts, example questions & explanations for GRE Math

Create An Account

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #871 : Gre Quantitative Reasoning

A college student takes out a loan of $8,000 per Quarter. A college student's average living cost is represented by the chart below.

Living_cost_per_quarter

Suppose tution is increased by 8%. What is the increase in the percentage of the loan that is spent on tutition and books?

Possible Answers:

$.03\%$

$3.88\%$

$60.97\%$

$8\%$

Correct answer:

$3.88\%$

Explanation:

The original percentage of the loan spent on tutition and books is 57.09%. After the 8% increase in tutition, the percentage of the loan is 60.97%

$P=\frac{[(3879.24)(1.08) + 687.92]}{8000}=.6097$

Thus, the increase in percentage is $60.97\%-57.09\%=3.88\%$ .

Report an Error

Example Question #872 : Gre Quantitative Reasoning

Untitled

By what percentage did the total book sales of the three stores increase from 2005 to 2010?

Possible Answers:

$\dpi{100} \small 33.3\%$

$\dpi{100} \small 25\%$

$\dpi{100} \small 15\%$

$\dpi{100} \small 20\%$

$\dpi{100} \small 12\%$

Correct answer:

$\dpi{100} \small 20\%$

Explanation:

Find the total number of books sold in 2005: 8 + 12 + 10 = 30 thousand

Find the total number of books sold in 2010: 11 + 13 + 12 = 36 thousand

$\dpi{100} \small Percent\ increase = \frac{(final - original)}{original} \times 100$

$\dpi{100} \small = \frac{(36 - 30)}{30} \times 100 = \frac{600}{30} = 20\%$

Report an Error

Example Question #4 : Percent Of Change

Which of the following is $\dpi{100} \small 550\%$ greater than $\dpi{100} \small 8\times 10^{3}$ ?

Possible Answers:

$\dpi{100} \small 5.2\times 10^{4}$

$\dpi{100} \small 7.6\times 10^{4}$

$\dpi{100} \small 5.4\times 10^{5}$

$\dpi{100} \small 6.8\times 10^{4}$

$\dpi{100} \small 1.6\times 10^{5}$

Correct answer:

$\dpi{100} \small 5.2\times 10^{4}$

Explanation:

The value of $\dpi{100} \small 8\times 10^{3}= 8000$

$\dpi{100} \small 8000+8000\times 550\%=8000+44,000=52,000$ .

In scientific notation, this is $\dpi{100} \small 5.2\times 10^{4}$ .

Report an Error

Example Question #283 : Arithmetic

A new painting company, Paintz, reported a profit of six thousand dollars in 2011. In 2012, Paintz reported $10,000 more profit than 2011. What was the percentage increase in profit for Paintz between 2011 and 2012?

Possible Answers:

$\dpi{100} \small 60\%$

$\dpi{100} \small 66.67\%$

$\dpi{100} \small 100\%$

$\dpi{100} \small 133.33\%$ %

$\dpi{100} \small 166.67\%$

Correct answer:

$\dpi{100} \small 166.67\%$

Explanation:

The formula for percentage increase is the difference in profit divided by the original profit multiplied by 100. Here the difference in profit between 2011 and 2012 is 10,000 and the original profit in 2012 is 6000, therefore the percentage increase is $\dpi{100} \small \frac{10,000}{6000}\times 100=166.67\%$ .

Report an Error

Example Question #873 : Gre Quantitative Reasoning

A city originally had a $6\%$ sales tax, but increased it to $8\%$ . Assuming that the rate of consumption in the city does not change, what was the total amount of sales tax collected when the rate was $6\%$ if the increase in tax brought in an additional $\$150,000$ in revenue?

Possible Answers:

$\$500,000$

$\$7,500,000$

$\$1,200,000$

$\$550,000$

$\$450,000$

Correct answer:

$\$450,000$

Explanation:

One way to solve this is by considering that the increase in taxes is a linear addition of 2%. Therefore we can ask the question, 2% of what amount yields $150,000? This can be represented in the following equation:

0.02 * x = 150,000

Solve for x: $7,500,000

Therefore, the total at the old rate is 7,500,000 * 0.06 = $450,000.

Report an Error

Example Question #12 : How To Find The Percent Of Increase

In 2014, approximately $27.7\%$ of Americans were considered charming. In 2013 approximately 27.1% of Americans were deemed charming. If the population of America in 2013 was $\textup{316.5 million}$ people and the population of America in 2014 was roughly $\textup{318.9 million}$ people, what is the percent increase/decrease of charming people from 2013-2014? Round to the nearest tenth.

Possible Answers:

$0.6\%$

$2.9\%$

$\textup{Cannot be determined with the information provided}$

$3.0\%$

$3.1\%$

Correct answer:

$3.0\%$

Explanation:

To solve this problem, we must understand that we can't simply use the percentage change from 2013-2014 in order to solve this problem. Because the populations change, simply using the percentage change in order to is invalid. Therefore we must find the amount of people that were charming in each year to solve for this problem.

In 2013, $27.1\%$ of the $\textup{316.5 million}$ people in America were considered charming, this means that the number of charming people in America in 2013 is 0.271*316.5=85.7715 $\textup{million}$ people.

In 2014, $27.7\%$ of the $\textup{318.9 million}$ people in America were considered charming, this means that the number of charming people in America in 2014 is 0.277*318.9=88.3353 $\textup{million}$ people.

Therefore to find the percent increase of charming people, we simply find the difference in charming people from 2013-2014 and divide by the number of charming people in 2013. $\frac{88.3353-85.7715}{85.7715}=\frac{2.5638}{85.7715}=0.02989$ or a $2.989\%$ increase in charming people.

Report an Error

Example Question #72 : Percentage

A new TV at some store goes on sale for $10\%$ off the retail price. A customer comes in to buy the TV, and in addition to the store discount of $10\%$ , uses a coupon for an extra $\$200$ off. The customer ends up paying $65\%$ of the original price of the TV. What is the original price of the TV?

Possible Answers:

$\$1050$

$\$750$

$\$1000$

$\$700$

$\$800$

Correct answer:

$\$800$

Explanation:

Let represent the original price of the TV. Now, set up an equation where the discounted price of the TV (10% discount) minus 200 dollars is equal to 65% of the original price of the TV:

0.9x-200=.65x

Solve for

0.9x-200+200=0.65x+200

0.9x=0.65x+200

0.9x-0.65x=200

0.25x=200

x=800

The original price of the TV is $\$800$ .

Report an Error

Example Question #1 : Sale Prices

A winter shirt is regularly priced at $50. At the end of the Christmas season, it is marked down by 40%. A month after this initial markdown, it is marked back up by 50%.

Quantity A

The initial cost of the shirt.

Quantity B

The final cost of the shirt, after it is marked up.

Possible Answers:

Quantity A is greater.

The quantities are equal.

Quantity B is greater.

The relationship cannot be determined from the information given.

Correct answer:

Quantity A is greater.

Explanation:

There are two ways to consider the value of B. First, you can subtract 40% from the initial $50 dollars: $50 – 0.4 * $50 = $30. This gives you the value after the markdown. Then to mark up the price, add 50% of $30 to the $30: $30 + 0.5 * $30 = $45.

A shorter way to do this problem is to consider the first markdown as reducing the price to 60% of the original, then considering the markup as making it 150% of the new price. This can be done in one set of multiplications: $50 * 0.6 * 1.5 = $45. Either way, the answer is the same. A is the larger quantity.

Report an Error

Example Question #1 : Sale Prices

A store puts a $200 dress on a 70% discount and then takes an additional 15% off the reduced price. How much of the original price was removed?

Possible Answers:

$30

$51

$149

$161

$170

Correct answer:

$149

Explanation:

If we multiply $200 by 0.7, we find the dress has been reduced by $140 on the first discount. Since the dress now costs $60, we multiply that by 0.15 and find the dress has been discounted by an additional $9. The final sale of the dress is $51, with $149 of the original price removed.

Report an Error

Example Question #74 : Percentage

In a local store, pens that normally sell for 49 cents each are on sale at 3 for 99 cents. How much can be saved by purchasing 12 of these pens at the sale price?

Possible Answers:

$1.44

$3.00

$2.04

$1.92

$2.00

Correct answer:

$1.92

Explanation:

Normally, 3 pens cost 3 * .49 = $1.47. Thus, on each set of 3 pens, the sale price saves the customer $1.47 - 99 = 48 cents. Multiply this by 4 to get the savings for 12 pens, and you get .48 * 4 = $1.92.

Report an Error

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Phoenix, Chemistry Tutors in Seattle, Biology Tutors in New York City, Spanish Tutors in Chicago, Biology Tutors in Seattle, English Tutors in Denver, French Tutors in San Francisco-Bay Area, LSAT Tutors in San Diego, SSAT Tutors in Phoenix, GRE Tutors in Philadelphia

Popular Courses & Classes

ISEE Courses & Classes in New York City, LSAT Courses & Classes in Houston, SAT Courses & Classes in Los Angeles, MCAT Courses & Classes in Houston, LSAT Courses & Classes in Phoenix, ISEE Courses & Classes in Boston, ACT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Washington DC, LSAT Courses & Classes in New York City, MCAT Courses & Classes in Philadelphia

Popular Test Prep

LSAT Test Prep in Denver, ISEE Test Prep in New York City, LSAT Test Prep in Dallas Fort Worth, ACT Test Prep in San Francisco-Bay Area, MCAT Test Prep in Denver, LSAT Test Prep in San Francisco-Bay Area, SAT Test Prep in Seattle, SSAT Test Prep in Seattle, SAT Test Prep in Philadelphia, GRE Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

Email address:
Your name:
Feedback:

GRE Math : GRE Quantitative Reasoning

Study concepts, example questions & explanations for GRE Math

All GRE Math Resources

Example Questions

Example Question #871 : Gre Quantitative Reasoning

Example Question #872 : Gre Quantitative Reasoning

Example Question #4 : Percent Of Change

Example Question #283 : Arithmetic

Example Question #873 : Gre Quantitative Reasoning

Example Question #12 : How To Find The Percent Of Increase

Example Question #72 : Percentage

Example Question #1 : Sale Prices

Example Question #1 : Sale Prices

Example Question #74 : Percentage

All GRE Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details