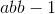All GRE Math Resources
Example Questions
Example Question #163 : Arithmetic
Solve for 
To solve, first isolate your variable by dividing both sides of the equation by 
As a check, if you divide an odd number by another odd number, your result should be odd.
Example Question #1 : How To Divide Odd Numbers
Solve for 
To solve, divide both sides of the equation by 
As a check, if you divide an odd number by another odd number, your result should be odd.
Example Question #1 : How To Multiply Odd Numbers
If 

With many questions like this, it might be easier to plug in numbers rather than dealing with theoretical variables. However, given that this question asks for the expression that is not always even or odd but only not necessarily odd, the theoretical route might be our only choice.
Therefore, our best approach is to simply analyze each answer choice.













Example Question #1 : Integers
Theodore has 
To find the answer to this question, calculate the total jelly beans for each person:
Portia: 

Harvey: 

So, the total is:
(Do not forget that you need those original 
Example Question #1 : How To Multiply Odd Numbers
Assume 

What is a possible solution for 
When two odd whole numbers are multipliedd, they will equal an odd whole number. The only answer that fits the requirements of being an odd and a whole number is 


Example Question #21 : Even / Odd Numbers
If 

To solve, pick numbers to represent 




Only 
Example Question #22 : Even / Odd Numbers


Quantity A:
The remainder of
Quantity B:
1
Quantity B is larger.
The two quantities are equal.
Quantity A is larger.
The relationship between the quantities cannot be determined.
Quantity B is larger.
Begin by considering our options. For 






Now, for 




Now, for 

Therefore, 


Therefore, quantity B is larger.
Example Question #1601 : Act Math


Therefore, which of the following must be true about 
It must be odd.
It could be either even or odd.
It must be even.
It could be either even or odd.
Recall that when you multiply by an even number, you get an even product.
Therefore, we know the following from the first statement:




For the second, we know this:
Since 


Based on all this data, we can tell nothing necessarily about 






Example Question #2 : How To Multiply Even Numbers
In a group of philosophers, 
In a group of philosophers, 
To start, let's calculate the total philosophers:
Ockham: 
Aquinas: 
Scotus: 

Therefore, the total number is:
Example Question #31 : Even / Odd Numbers
Assume 

What is a possible solution for 
When two even numbers are multiplied, they must equal an even number. Also, since both variables are said to be even whole numbers, the answer must fit the requirement that its factors are two even numbers multiplied by one another. The only answer that fits both requirements is 


All GRE Math Resources