All GRE Math Resources
Example Questions
Example Question #1 : How To Find Out A Mixed Fraction From An Improper Fraction
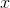
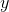
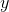
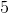
Quantity A:
Quantity B:
The two quantities are equal.
The relationship cannot be determined.
Quantity B is greater.
Quantity A is greater.
The relationship cannot be determined.
Recall that the exponent of the denominator is sutracted from the exponent of the numerator.
Therefore Quantity A is equivalent to x5–y, and because we would then be comparing an arithmetic operation to a geometric operation, it does not matter whether y is a multiple of 5. The two quantities cannot be compared.
Example Question #136 : Fractions
Which of the following is the mixed fraction equivalent to 
To begin, notice that using your calculator, you can find:
Now, the closest even multiple of 


This is the same as:


Example Question #3 : Mixed / Improper Fractions
Which of the following is equivalent to 
Although there are many ways to convert improper fractions into mixed fractions, the easiest way is to use your calculator to your advantage. Begin by dividing 










Example Question #1 : How To Find Out A Mixed Fraction From An Improper Fraction
Quantity A:
Quantity B:
Which of the following is true?
Quantity A is larger.
Quantity B is larger.
The relationship of the two quantities cannot be determined based on the information provided.
The two quantities are equal
The two quantities are equal
Though there are several ways you could solve this, let's convert the improper fraction into a mixed one so we can compare them. Start by dividing 


Now, since we know that the two numbers have the same whole-number value, we need to compare their decimal portions. Compare 


Example Question #132 : Fractions
Write 
To find the improper fraction value, we must effectively add together 71 and 5/7. To do this, we will give 71 a denominator of 7; therefore, we are transforming 71/1 to x/7. The shortest way to do this is to multiply by 7/7 (which really is 1); therefore, 71 = 71 * (7/7) = 497/7.
Now add them: (497 + 5)/7 = 502/7
Example Question #133 : Fractions
Which of the following improper fractions is equivalent to 
To find an improper fraction, you need to multiply the whole number that you have by the denominator of the associated fraction. For our problem, this means that you will multiply 




Example Question #2 : Mixed / Improper Fractions
Which of the following improper fractions is equivalent to 
To find an improper fraction, you need to multiply the whole number that you have by the denominator of the associated fraction. For our problem, this means that you will multiply 




Example Question #71 : Fractions
In terms of 



The arithmetic mean of a set is defined as the sum of terms in the set divided by the number of terms of a set. Therefore, the mean for this problem can be found as:
Example Question #72 : Fractions
Harold is drawing numbered slips of paper from a hat that are labeled 

There are 


The probability of one being drawn is 



For this sequence of events to happen, the probability is the product of the three separate probabilities:
Example Question #73 : Fractions
Happy Harold's Creamery offers specials during the week on particular sundaes. Monday they offer the Triple Trouble, in which three different scoops may be chosen from the full thirty-one that HHC offers. Tuesday features, for the same price, the Fearsome Four, which is a sundae of four scoops; however, only twenty-one flavors may be chosen from.
Quantity A: The amount of sundae options available for the Triple Trouble.
Quantity B: The amount of sundae options available for the Fearsome Four.
The relationship between the two cannot be determined.
The two quantities are equal.
Quantity A is greater.
Quantity B is greater.
Quantity B is greater.
Both of these sundae options are dealing with combinations, i.e. the order the scoops are chosen does not matter, and so the amount of possible combos is given by the formula:
Where 

For the Triple Trouble, the total amount of possible sundaes is:
And for the Fearsome Four:

All GRE Math Resources



















































