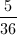First we want to find the fraction of employees that neither take the bus nor drive, so we’ll add the fractions that do take the bus or drive and subtract that result from the total.

Bus:

Drive:

Remaining:

Now we need the fraction representing one third of these remaining employees (the fraction that ride a bike). Since "of " means multiply, we'll multiply.

Multiplying fractions is very easy. All you do is multiply all the numerators by each other and all the denominators by each other. You do not have to do anything that has to do with fancy common denominators like you do for adding and subtracting. For a question like this, it is often easiest just to cancel factors before you start your final multiplication. First, note:

Now, cancel the  from the :

Next, the  in the numerator cancels with the  in the denominator:

Finally, the  in the numerator cancels with the  in the denominator:

Multiplying fractions is very easy. All you do is multiply all the numerators by each other and all the denominators by each other. You do not have to do anything that has to do with fancy common denominators like you do for adding and subtracting. For a question like this, it is often easiest just to cancel factors before you start your final multiplication. First, note:

Now, cancel the  in the denominator with the  in the numerator:

Next, the  in the numerator cancels with the  in the denominator:

Finally, cancel the  in the denominator with the  in the numerator:

Begin by distributing the group on the left side of the equation. Remember that it is easy to multiply fractions. You only need to multiply the denominators and numerators. There are no "fancy" steps in between.

Therefore,

is the same as:

You can cancel part of the second fraction out, so you get:

Now, subtract  from both sides:

Simplifying the right side of the equation, you get...

Now, multiply both sides by :

Simplify:

Let's make the two quantities look the same. 

Quantity A: 120 miles / 5 gallons =  24 miles / gallon

Quantity B: 25 miles / gallon

Quantity B is greater.

In order to solve quantitative comparison problems, you must first deduce whether or not the problem is actually solvable. Since this consists of finding the solution to an -coordinate on a line where nothing too complicated occurs, it will be possible.  

Thus, your next step is to solve the problem.

Since  and , you can plug in the -value and solve for :

Plug in y:

Add 2 to both sides:

Divide by 3/4.  To divide, first take the reciprocal of 3/4 (aka, flip it) to get 4/3, then multiply that by 5/3:

Make the improper fraction a mixed number:

 Now that you have what x equals, you can compare it to Quantity B. 

Since  is bigger than 2, the answer is that Quantity A is greater

Remember that when you divide by a fraction, you multiply by the reciprocal of that fraction.  Therefore, this division really is:

At this point, it is merely a matter of simplification and finishing the multiplication:

To begin with, most students find it easy to remember that...

From this, you can apply the rule of division of fractions.  That is, multiply by the reciprocal:

Therefore,

Since nothing needs to be reduced, this is your answer.

Write their respective rates as fractions:

Carpenter A:

Carpenter B:

Add them together to find their combined rate.  First find a common denominator.  The smallest multiple of both 45 and 30 is 90:

Therefore, they take 18 hours to build a table together.