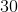It is important to realize that this problem deals with combinations, rather than permutations; the order the shirts are drawn does not matter. That being said, the formula for a combination is given as:

Where  is the total number of options and  is the size of the combination created.

Quantity A:

Quantity B:

To solve this problem, you may find the total distance traveled and divide that by the total time taken.  The distance traveled in miles is:

Since the trip took  hours in total, Ron's average speed in miles per hour is:

The average, or arithmetic mean, of a set can be found by dividing the sum of the set by the amount of values in the set:

The median for a set depends on if there's an even or odd number of values in the set.

For an odd number of values in a set that is arranged in numerical order, , the median is given as the middle value, .

For an even number of values in a set that is again arranged in numerical order, ,there is no value exactly in the middle; rather there are two. The median is then given as the average of these two values:

Rearranging the set into numerical order gives , thus the median is 

First solve for z by multiplying 2/7 by the reciprocal of 4/13. 

Then multiply this number by 8/11 to find the solution.

In setting up the problem, notice how “of” means to multiply z by 4/13 and “is” means to set (4/13)z equal to 2/7.

If 3 senior men = 30% * All Men →

All Men = 3/30% = 10 Men. 

The Ratio Men : Women = 5 : 3 = 10 : 6.

Thus there are 6 Women. 6 + 10 = 16. 

Say cost of each pair of socks = y and pairs of socks = x.

Since [quantity x cost per item = total cost]:

First, xy = 50.

Secondly, (x + 5) [y (1 - 20%)] = 50

Simplify the second equation:

 80%y(x + 5) = 50 or

 0.8xy + 4y = 50

Insert xy =50 here.

.8(50) + 4y = 50

40 + 4y = 50 or 4y = 10

Thus y = 10/4 = 5/2

Need to find x = pairs of socks. 

xy = 50 = x(5/2)

So 5x = 100 or x = 20

This problem requires you to work backwards from stop 5 to the passengers present at stop 1. If 2 person gets out at stop 5, that means there were 3 people on board at stop 5. This means there were 9 people present at stop 4 (9 total, 2/3 (6) got off, leaving the 3 for stop 5), 27 people present at stop 3 (27 total, 2/3 (18) got off, leaving 9 for stop 4), 81 people present at stop 2 and 243 passengers present at stop 1. That is, the number of passengers on board the train at any stop follows a logarithmic reduction along powers of three, from 3⁵ at stop 1 to 3¹ at stop 5.

We need to convert 5 hours into minutes. There are 60 minutes in an hour, so 5 hours = 5 * 60 minutes = 300 minutes. Therefore, you go 20 meters/minute for 300 minutes, or 20 * 300 = 6000 meters.

21.21/ 4.25 = 5 pounds paid for.  Since a pound is given for every 2 pounds sold, that is 5/2 = 2.5 so an extra 2 pounds is given to Lauren, totaling 7 pounds.

Since Bob and Nancy work at the same rate, each person can finish  of the job in 3 hours. Because 45 minutes is  of 3 hours, Bob working alone would get  of the job done, .