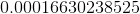GRE Math : Arithmetic
Study concepts, example questions & explanations for GRE Math
All GRE Math Resources
Example Questions
Example Question #1 : How To Find Absolute Value
Quantitative Comparison
|x – 3| = 3
Quantity A: x
Quantity B: 2
Quantity A is greater.
The relationship cannot be determined from the information given.
Quantity B is greater.
The two quantities are equal.
The relationship cannot be determined from the information given.
It's important to remember that absolute value functions yield two equations, not just one. Here we have x – 3 = 3 AND x – 3 = –3.
Therefore x = 6 or x = 0, so the answer cannot be determined.
If we had just used the quation x – 3 = 3 and forgotten about the second equation, we would have had x = 6 as the only solution, giving us the wrong answer.
Example Question #211 : Arithmetic
Quantitative Comparison
Quantity A: |10| – |16|
Quantity B: |1 – 5| – |3 – 6|
The relationship cannot be determined from the information given.
Quantity A is greater.
Quantity B is greater.
The two quantities are equal.
Quantity B is greater.
Quantity A: |10| = 10, |16| = 16, so |10| – |16| = 10 – 16 = –6.
Quantity B: |1 – 5| = 4, |3 – 6| = 3, so |1 – 5| - |3 – 6| = 4 – 3 = 1.
1 is bigger than –6, so Quantity B is greater.
Example Question #794 : Gre Quantitative Reasoning
Quantitative Comparison
Quantity A: (|–4 + 1| + |–10|)2
Quantity B: |(–4 + 1 – 10)2|
The two quantities are equal.
Quantity A is greater.
Quantity B is greater.
The relationship cannot be determined from the information given.
The two quantities are equal.
Quantity A: |–4 + 1| = |–3| = 3 and |–10| = 10, so (|–4 + 1| + |–10|)2 = (3 + 10)2 = 132 = 169
Quantity B: |(–4 + 1 – 10)2| = |(–13)2| = 169
The two quantities are equal.
Example Question #142 : Integers
Quantity A:
Quantity B:
The relationship cannot be determined from the information given
Quantity B is greater
Quantity A is greater
The two quantities are equal
Quantity B is greater
If 
Example Question #143 : Integers
What is the absolute value of the following equation when 
(–3)3 = –27. Any time a negative number is cubed, it remains negative. –27 + 5 = –22. The absolute value of any number will ALWAYS be positive so the absolute value of –22 is 22. This is our answer.
Example Question #212 : Arithmetic
Evaluate:
3 + 2(1 * 9 + 8) – 9/3
36
76/3
34
37/3
82
34
Order of operations
Do everything inside the parenthesis first:
3 + 2(17) – 9/3
next, do multiplication/division
3 + 34 – 3
= 34
Example Question #151 : Integers
3 + 4 * 5 / 10 – 2 =
5.5
7
3
5
1.5
3
Here we must use order of operations. First we multiply 4 * 5 = 20. Then 20 / 10 = 2. Now we can do the addition and substraction. 3 + 2 – 2 = 3. If you started at the beginning on the left hand side and not used order of operations, you would mistakenly choose 1.5 as the correct answer.
Example Question #801 : Gre Quantitative Reasoning
Order of operations can be remembered by PEMDAS (Please Excuse My Dear Aunt Sally): Parentheses Exponents Multiplication Division Addition Subtraction.
[7(5 + 2) – (5 * 8)]2 =
1: Inner parentheses = [ 7(7) – 40 ]2
2: Outer brackets = [ 49 – 40 ]2 = 92
3: Exponents = 81
Example Question #802 : Gre Quantitative Reasoning
This looks daunting as one long equation, but let's look at each piece and then add them all together.
2–3 = 1/23 = 1/8
250 = 1
(–218)1 = –218
6251/4 = 5
(–27)1/3 = –3
Then, 2–3 + 250 + (–218)1 + 7/8 – 6251/4 + (–27)1/3 = 1/8 + 1 – 218 + 7/8 – 5 – 3 = –224.
Example Question #1 : Percentage
What percentage of a solution is blood if it contains 
First, you must find the total amount of solution. This is 
Now, the percentage of the solution that is blood can be represented:
This is the same as 
All GRE Math Resources
