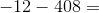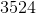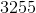Calculate the difference in thousands of sales for each store individually:

Store A:  thousand

Store B:  thousand

Store C:  thousand

Stores A and B both had a 5000-book increase in sales, so A and B tie.

If it helps, for this problem, think about starting at 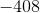 and moving twelve places in a negative direction away from zero.  

Also you can think to add 408 with 12 and then multiply that number by a negative one. Starting with the ones place eight plus two gives ten so we keep the zero in the ones place and carry the one to the tens place. Then we add one plus one to give us a two in the tens column. Next we have a four in the hundreds place. This gives us 420. Now we multiply this by negtive one to get our final answer of -420.

Whenever you subtract a negative number, you flip the sign and add:

There are 50 positive, odd numbers less than 100, and 45 of them are 2 digit numbers.

Since:

1. There are only 9 integers between 0 and 10
2. x, y, and z must all be unique
3. They must be specifically ordered such that x < y < z

There are actually not too many ways in which these numbers can be chosen. So what we can do is find a range of answers for Quantity B, and see if 6 falls a) below b) above or c) in between the range.

For the maximum:

Note that the term (x + y) is maximized when x and y are maximum. The (–z) term is maximized when z is minimized. However, there are 2 terms in (x + y) and one term in (–z); thus intuitively it seems we should prioritize (x+y). To make x and y maximum:

0 < 7 < 8 < 9 < 10 since x, y, and z must be unique.

Thus maximum: (x + y – z) = 7 + 8 – 9 = 6

For the minimum:

Note that (x + y) is minimum when (x) and (y) are minimum, and (–z) is minimum when (z) itself is maximimized. However since there are 2 terms in (x+y) and1 of (–z) , again intuititively you should prioritize  (x+y) over (-z). Then in order to make this the least number possible, x and y would be:

min(x + y – z) = 1 + 2 – 9 = –6  

Thus, the range of possible answers is:

(x + y – z): [–6, 6] 

and –7 is always less than this amount.

The question asks for the number of positive even and odd integers less than 1000. Because 1000 is not included, the numbers to consider are 1 through 999. Every positive odd integer will have a corresponding even integer (1 and 2, 3 and 4, 5 and 6, etc.) until you get to 999. This gives the positive odd integers one more number than the number of positive even integers.

Miles is 3 years older than Ashley, so M = A + 3. Also, Bill is 5 years older than Ashley, so B = A + 5.  Together the three of their ages sum to 44, thus:

A + A + 3 + A + 5 = 44

3A + 8 = 44

3A = 36

A = 12

An integer with a units digit of 5 occurs once every 10 consecutive integers. There are 300 integers between 200 and 500, so there must be 30 values with a units digit of 5.

There are 13 "magic" numbers: 3,4,6,8,9,12, their negative counterparts, and 0.

The operations in the absolute value are always done first. So in Column A, |–3 + 4| = |1| = 1.  In Column B, |–3| + |4| = 3 + 4 = 7.