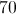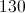When multiplying integers, if both of the signs of the integers are the same (positive, or negative) then your result will be positive:

First multiply the ones digit of both numbers together. If the product is greater than ten remember to carry the one to the tens place.

Next multiply the ones digit of the smaller number with the tens digit of the larger number and add the number that was carried over.

Combine these two together to get:

Simply recognize that logically, the participation of either sport is non-exclusive, that is, just because people took track and field does not necessarily mean they did not take swimming as well. As such, those 51 who took swimming could have all potentially done track and field, which means all 51 students.

There are 120 students in the math club and 150 students in the chess club, for a total membership of 270. However, 100 students are in both clubs, which means they are counted twice. You simply subtract 100 from 270, which will give you a total of 170 different students participating in both clubs. This means that the remaining 130 students do not participate in either club.

When adding integers, one needs to pay close attention to the sign.  When you add a negative integer, it's the same thing as subtracting that integer.  Therefore:

The sum of any two negative numbers will be negative.  Remember, also, that adding a negative number is like subtracting it.  Therefore: 

Because Sam needs to make 300 pies, and each pie needs 4 apples, the number of apples he needs is

300 x 4 = 1200.

To determine how many bushels Sam needs, divide the total number of apples by the number of apples sold in a bushel.

1200 / 126 = 9.524

Because apples are sold by the whole bushel, Sam cannot order part of a bushel. In order to make sure he has sufficient apples, he will need to order 10 bushels.

In order to find a number divisible by 6, you must find a number divisible by both of its factors — 2 and 3. Only even numbers are divisible by 2, so 81 is eliminated. In order to be divisible by 3, the sum of the digits has to be divisible by 3.

The sum of the digits of 316 is  3 + 1 + 6 = 10.

For 240, the sum is 2 + 4 = 6.

For 118, the sum is 1 + 1 + 8 = 10.

Only 6 is divisible by 3.

4 is already an integer, so we need to make sure x/10 is an integer too.  

Multiples of 5 won't work. For example, 5 is a multiple of 5 but 5/10 isn't an integer. Similarly, if x/10 leaves a remainder of 5, x/10 isn't an integer. For example, 15/10 leaves a remainder of 5 and isn't an integer.  

If x/10 has no remainder, then it must be an integer. For example, 10/10 and 20/10 both leave no remainders and simplify to the integers 1 and 2, respectively. 

If the remainder of  is , we know that  could be:

Since this generates an entire list of values, we cannot know which quantity is larger.  

Do not be tricked by the question, which is trying to get you to say that they are equal!

Begin by writing out a few possible values for  and .  

Since the remainder of  is , we can list:

Since the remainder of  is , we can list:

Since  (which is ) is your smallest possible value, you know that  and  are not options.  You cannot derive either  or  from the values given.  

Therefore, the only option that is left is , which is equal to .