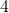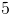GRE Math : Arithmetic
Study concepts, example questions & explanations for GRE Math
All GRE Math Resources
Example Questions
Example Question #4 : How To Divide Even Numbers
Solve for 
To solve, isolate the variable by dividing both sides of your equation by 
As a check, know that any time you divide an even number by another even number, your result will be even.
Example Question #111 : Integers
Assume 
What is a possible solution of 
Since 
Example Question #181 : Arithmetic
The product of two integers is 14. Which of the following could be the average of the two numbers?
The two integers in this case, and their respective averages, could be:
Only 
Example Question #181 : Arithmetic
Which of these is a natural number?
None of these are natural numbers .
All of these are natural numbers.
The natural numbers are the positive integers (whole numbers) starting with 1.
Example Question #182 : Arithmetic
Which of the following pairs of events are mutually exclusive?
the positive numbers, the numbers less than
the even numbers, the numbers greater than
the numbers less than 
the negative numbers,
the positive numbers, the numbers less than
We can think of mutually exclusive in terms of a Venn diagram. We are looking for the pair of events that has nothing in common. The only sets that don't have a single number in common are the positive numbers and the numbers less than –200.
Example Question #183 : Arithmetic
In the set of positive, distinct integers 
We know that all the numbers are positive, so they are greater than zero. We also know that the numbers are distinct, so they are all unique.
We can write this as {a + b + 8 + d + e}, so let a and b be 1 and 2 respectively, the smallest possible positive, distinct integers. Then let d and e be 9 and 10, the smallest positive, distinct integers larger than 8.
We add the set {1 + 2 + 8 + 9 + 10} to find it equals 30.
Example Question #772 : Gre Quantitative Reasoning
The product of two consecutive positive integers is 272. What is the larger of the two integers?
16
18
19
17
15
17
In order to multiply to 272, the units digits of the two integers will have to multiply to a number with a units digit of 2. For 17, you can see that 6 x 7 (the units digits of 16 and 17) = 42. The best strategy here is to plug in the choices using the units digit strategy.
Example Question #182 : Arithmetic
What is the units digit of 
The units digit of any product depends on the units digits of the 2 numbers multiplied, which in this case is 3 and 4. Since 
Example Question #121 : Integers
What is the units digit of
The units digit of the product of any two numbers is the same as the units digit of the product of the two numbers' units digits. In this case, it would be the units digit of 
Example Question #184 : Arithmetic
Choose the answer below which best solves the following equation:
When multiplying integers, if one of the integers is negative, your answer will be negative:
First multiply the ones digits together.
Next multiply the ones digit of the smaller number with the tens digit of the larger number to get the tens digit of the product.
Combining these two and remembering the negative sign we get our final answer:
All GRE Math Resources
