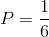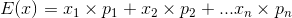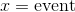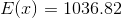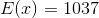All Common Core: High School - Statistics and Probability Resources
Example Questions
Example Question #4 : Evaluate And Compare Strategies Of Expected Values: Ccss.Math.Content.Hss Md.B.5b
A motorist is attempting to decide between the following two insurance policies:
A deductible is the amount of money that you have to pay out-of-pocket before your insurance company will cover the rest. In other words, if the total cost of an accident is and you have a deductible, then you will pay for the accident and your insurance will cover the remaining .
Consider the following:
Given this information which policy can we expect will save the motorist the most money in the following year?
Cannot be determined
The low deductible policy is cheaper by
The low deductible policy is cheaper by
The high deductible policy is cheaper by
The high deductible policy is cheaper by
The low deductible policy is cheaper by
This substandard specifically relates to strategies that can be used to evaluate and compare strategies associated with expected values. This means that we will use our knowledge of probabilities and expected values to evaluate between options and make informed decisions on which will be more profitable in the long run. As a result, this standard relies on an understanding of probabilities as well as the expected means formula. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
In this equation the variables are identified as the following:
We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle owner's engine size with its respective probability and solve.
Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:
Round to the nearest one's place.
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Now, lets use this information to solve the problem. We will use the expected means formula and substitute the variable for the expected amount of money to be paid in the long run for each insurance policy given the probability of a minor and major accident. Let's start by calculating the expected expense associated with a high deductible insurance policy. Let's start by figuring out the expense for both the major and minor accidents associated with a high deductible policy. For the minor accident, the amount of the damage is less than the deductible; therefore, the entire amount must be paid by the motorist. Conversely, on the major accident, the motorist only needs to pay the complete deductible; therefore, we can write the following formula:
Substitute in our known values.
Solve.
Now, we need to add in the total cost of the policy for the year by adding in the sum of the monthly payments of the policy in a given year.
Next, we need to calculate the expected expense associated with a low deductible insurance policy. Let's start by figuring out the expense for both the major and minor accidents associated with a low deductible policy. For the minor accident, the amount of the damage is more than the deductible; therefore, the motorist only pays the low deductible. Likewise, on the major accident, the motorist only needs to pay the deductible; therefore, we can write the following formula:
Substitute in our known values.
Solve.
Now, we need to add in the total cost of the policy for the year by adding in the sum of the monthly payments of the policy in a given year.
Last, we need to subtract the expected expense of the high deductible policy from the lower one in order to calculate how much cheaper the lower deductible policy is.
The correct choice is the following:
The low deductible policy is cheaper by
Example Question #5 : Evaluate And Compare Strategies Of Expected Values: Ccss.Math.Content.Hss Md.B.5b
A motorist is attempting to decide between the following two insurance policies:
A deductible is the amount of money that you have to pay out-of-pocket before your insurance company will cover the rest. In other words, if the total cost of an accident is and you have a deductible, then you will pay for the accident and your insurance will cover the remaining .
Consider the following:
Given this information which policy can we expect will save the motorist the most money in the following year?
Cannot be determined
The low deductible policy is cheaper by
The low deductible policy is cheaper by
The high deductible policy is cheaper by
The high deductible policy is cheaper by
The low deductible policy is cheaper by
This substandard specifically relates to strategies that can be used to evaluate and compare strategies associated with expected values. This means that we will use our knowledge of probabilities and expected values to evaluate between options and make informed decisions on which will be more profitable in the long run. As a result, this standard relies on an understanding of probabilities as well as the expected means formula. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
In this equation the variables are identified as the following:
We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle owner's engine size with its respective probability and solve.
Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:
Round to the nearest one's place.
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Now, lets use this information to solve the problem. We will use the expected means formula and substitute the variable for the expected amount of money to be paid in the long run for each insurance policy given the probability of a minor and major accident. Let's start by calculating the expected expense associated with a high deductible insurance policy. Let's start by figuring out the expense for both the major and minor accidents associated with a high deductible policy. For the minor accident, the amount of the damage is less than the deductible; therefore, the entire amount must be paid by the motorist. Conversely, on the major accident, the motorist only needs to pay the complete deductible; therefore, we can write the following formula:
Substitute in our known values.
Solve.
Now, we need to add in the total cost of the policy for the year by adding in the sum of the monthly payments of the policy in a given year.
Next, we need to calculate the expected expense associated with a low deductible insurance policy. Let's start by figuring out the expense for both the major and minor accidents associated with a low deductible policy. For the minor accident, the amount of the damage is more than the deductible; therefore, the motorist only pays the low deductible. Likewise, on the major accident, the motorist only needs to pay the deductible; therefore, we can write the following formula:
Substitute in our known values.
Solve.
Now, we need to add in the total cost of the policy for the year by adding in the sum of the monthly payments of the policy in a given year.
E(low\ deductible)=\$ 1715.0
Last, we need to subtract the expected expense of the high deductible policy from the lower one in order to calculate how much cheaper the lower deductible policy is.
The correct choice is the following:
The low deductible policy is cheaper by
Example Question #6 : Evaluate And Compare Strategies Of Expected Values: Ccss.Math.Content.Hss Md.B.5b
A motorist is attempting to decide between the following two insurance policies:
A deductible is the amount of money that you have to pay out-of-pocket before your insurance company will cover the rest. In other words, if the total cost of an accident is and you have a deductible, then you will pay for the accident and your insurance will cover the remaining .
Consider the following:
Given this information which policy can we expect will save the motorist the most money in the following year?
The high deductible policy is cheaper by
The high deductible policy is cheaper by
Cannot be determined
The low deductible policy is cheaper by
The low deductible policy is cheaper by
The low deductible policy is cheaper by
This substandard specifically relates to strategies that can be used to evaluate and compare strategies associated with expected values. This means that we will use our knowledge of probabilities and expected values to evaluate between options and make informed decisions on which will be more profitable in the long run. As a result, this standard relies on an understanding of probabilities as well as the expected means formula. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
In this equation the variables are identified as the following:
We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle owner's engine size with its respective probability and solve.
Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:
Round to the nearest one's place.
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Now, lets use this information to solve the problem. We will use the expected means formula and substitute the variable for the expected amount of money to be paid in the long run for each insurance policy given the probability of a minor and major accident. Let's start by calculating the expected expense associated with a high deductible insurance policy. Let's start by figuring out the expense for both the major and minor accidents associated with a high deductible policy. For the minor accident, the amount of the damage is less than the deductible; therefore, the entire amount must be paid by the motorist. Conversely, on the major accident, the motorist only needs to pay the complete deductible; therefore, we can write the following formula:
Substitute in our known values.
Solve.
Now, we need to add in the total cost of the policy for the year by adding in the sum of the monthly payments of the policy in a given year.
Next, we need to calculate the expected expense associated with a low deductible insurance policy. Let's start by figuring out the expense for both the major and minor accidents associated with a low deductible policy. For the minor accident, the amount of the damage is more than the deductible; therefore, the motorist only pays the low deductible. Likewise, on the major accident, the motorist only needs to pay the deductible; therefore, we can write the following formula:
Substitute in our known values.
Solve.
Now, we need to add in the total cost of the policy for the year by adding in the sum of the monthly payments of the policy in a given year.
Last, we need to subtract the expected expense of the high deductible policy from the lower one in order to calculate how much cheaper the lower deductible policy is.
The correct choice is the following:
The low deductible policy is cheaper by
Example Question #7 : Evaluate And Compare Strategies Of Expected Values: Ccss.Math.Content.Hss Md.B.5b
A motorist is attempting to decide between the following two insurance policies:
A deductible is the amount of money that you have to pay out-of-pocket before your insurance company will cover the rest. In other words, if the total cost of an accident is and you have a deductible, then you will pay for the accident and your insurance will cover the remaining .
Consider the following:
Given this information which policy can we expect will save the motorist the most money in the following year?
The low deductible policy is cheaper by
The high deductible policy is cheaper by
Cannot be determined
The low deductible policy is cheaper by
The high deductible policy is cheaper by
The low deductible policy is cheaper by
This substandard specifically relates to strategies that can be used to evaluate and compare strategies associated with expected values. This means that we will use our knowledge of probabilities and expected values to evaluate between options and make informed decisions on which will be more profitable in the long run. As a result, this standard relies on an understanding of probabilities as well as the expected means formula. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
In this equation the variables are identified as the following:
We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle owner's engine size with its respective probability and solve.
Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:
Round to the nearest one's place.
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Now, lets use this information to solve the problem. We will use the expected means formula and substitute the variable for the expected amount of money to be paid in the long run for each insurance policy given the probability of a minor and major accident. Let's start by calculating the expected expense associated with a high deductible insurance policy. Let's start by figuring out the expense for both the major and minor accidents associated with a high deductible policy. For the minor accident, the amount of the damage is less than the deductible; therefore, the entire amount must be paid by the motorist. Conversely, on the major accident, the motorist only needs to pay the complete deductible; therefore, we can write the following formula:
Substitute in our known values.
Solve.
Now, we need to add in the total cost of the policy for the year by adding in the sum of the monthly payments of the policy in a given year.
Next, we need to calculate the expected expense associated with a low deductible insurance policy. Let's start by figuring out the expense for both the major and minor accidents associated with a low deductible policy. For the minor accident, the amount of the damage is more than the deductible; therefore, the motorist only pays the low deductible. Likewise, on the major accident, the motorist only needs to pay the deductible; therefore, we can write the following formula:
Substitute in our known values.
Solve.
Now, we need to add in the total cost of the policy for the year by adding in the sum of the monthly payments of the policy in a given year.
Last, we need to subtract the expected expense of the high deductible policy from the lower one in order to calculate how much cheaper the lower deductible policy is.
The correct choice is the following:
The low deductible policy is cheaper by
Example Question #8 : Evaluate And Compare Strategies Of Expected Values: Ccss.Math.Content.Hss Md.B.5b
A motorist is attempting to decide between the following two insurance policies:
A deductible is the amount of money that you have to pay out-of-pocket before your insurance company will cover the rest. In other words, if the total cost of an accident is and you have a deductible, then you will pay \$1,000.00 for the accident and your insurance will cover the remaining .
Consider the following:
Given this information which policy can we expect will save the motorist the most money in the following year?
The high deductible policy is cheaper by
The high deductible policy is cheaper by
Cannot be determined
The low deductible policy is cheaper by
The low deductible policy is cheaper by
The low deductible policy is cheaper by
This substandard specifically relates to strategies that can be used to evaluate and compare strategies associated with expected values. This means that we will use our knowledge of probabilities and expected values to evaluate between options and make informed decisions on which will be more profitable in the long run. As a result, this standard relies on an understanding of probabilities as well as the expected means formula. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
In this equation the variables are identified as the following:
We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle owner's engine size with its respective probability and solve.
Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:
Round to the nearest one's place.
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Now, lets use this information to solve the problem. We will use the expected means formula and substitute the variable for the expected amount of money to be paid in the long run for each insurance policy given the probability of a minor and major accident. Let's start by calculating the expected expense associated with a high deductible insurance policy. Let's start by figuring out the expense for both the major and minor accidents associated with a high deductible policy. For the minor accident, the amount of the damage is less than the deductible; therefore, the entire amount must be paid by the motorist. Conversely, on the major accident, the motorist only needs to pay the complete deductible; therefore, we can write the following formula:
Substitute in our known values.
Solve.
Now, we need to add in the total cost of the policy for the year by adding in the sum of the monthly payments of the policy in a given year.
Next, we need to calculate the expected expense associated with a low deductible insurance policy. Let's start by figuring out the expense for both the major and minor accidents associated with a low deductible policy. For the minor accident, the amount of the damage is more than the deductible; therefore, the motorist only pays the low deductible. Likewise, on the major accident, the motorist only needs to pay the deductible; therefore, we can write the following formula:
Substitute in our known values.
Solve.
Now, we need to add in the total cost of the policy for the year by adding in the sum of the monthly payments of the policy in a given year.
Last, we need to subtract the expected expense of the high deductible policy from the lower one in order to calculate how much cheaper the lower deductible policy is.
The correct choice is the following:
The low deductible policy is cheaper by
Example Question #9 : Evaluate And Compare Strategies Of Expected Values: Ccss.Math.Content.Hss Md.B.5b
A motorist is attempting to decide between the following two insurance policies:
A deductible is the amount of money that you have to pay out-of-pocket before your insurance company will cover the rest. In other words, if the total cost of an accident is and you have a deductible, then you will pay for the accident and your insurance will cover the remaining .
Consider the following:
Given this information which policy can we expect will save the motorist the most money in the following year?
The high deductible policy is cheaper by
Cannot be determined
The high deductible policy is cheaper by
The low deductible policy is cheaper by
The low deductible policy is cheaper by
The low deductible policy is cheaper by
This substandard specifically relates to strategies that can be used to evaluate and compare strategies associated with expected values. This means that we will use our knowledge of probabilities and expected values to evaluate between options and make informed decisions on which will be more profitable in the long run. As a result, this standard relies on an understanding of probabilities as well as the expected means formula. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
In this equation the variables are identified as the following:
We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle owner's engine size with its respective probability and solve.
Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:
Round to the nearest one's place.
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Now, lets use this information to solve the problem. We will use the expected means formula and substitute the variable for the expected amount of money to be paid in the long run for each insurance policy given the probability of a minor and major accident. Let's start by calculating the expected expense associated with a high deductible insurance policy. Let's start by figuring out the expense for both the major and minor accidents associated with a high deductible policy. For the minor accident, the amount of the damage is less than the deductible; therefore, the entire amount must be paid by the motorist. Conversely, on the major accident, the motorist only needs to pay the complete deductible; therefore, we can write the following formula:
Substitute in our known values.
Solve.
Now, we need to add in the total cost of the policy for the year by adding in the sum of the monthly payments of the policy in a given year.
Next, we need to calculate the expected expense associated with a low deductible insurance policy. Let's start by figuring out the expense for both the major and minor accidents associated with a low deductible policy. For the minor accident, the amount of the damage is more than the deductible; therefore, the motorist only pays the low deductible. Likewise, on the major accident, the motorist only needs to pay the deductible; therefore, we can write the following formula:
Substitute in our known values.
Solve.
Now, we need to add in the total cost of the policy for the year by adding in the sum of the monthly payments of the policy in a given year.
Last, we need to subtract the expected expense of the high deductible policy from the lower one in order to calculate how much cheaper the lower deductible policy is.
The correct choice is the following:
The low deductible policy is cheaper by
Example Question #10 : Evaluate And Compare Strategies Of Expected Values: Ccss.Math.Content.Hss Md.B.5b
A motorist is attempting to decide between the following two insurance policies:
A deductible is the amount of money that you have to pay out-of-pocket before your insurance company will cover the rest. In other words, if the total cost of an accident is and you have a deductible, then you will pay for the accident and your insurance will cover the remaining .
Consider the following:
Given this information which policy can we expect will save the motorist the most money in the following year?
The low deductible policy is cheaper by
The high deductible policy is cheaper by
The high deductible policy is cheaper by
Cannot be determined
The low deductible policy is cheaper by
The low deductible policy is cheaper by
This substandard specifically relates to strategies that can be used to evaluate and compare strategies associated with expected values. This means that we will use our knowledge of probabilities and expected values to evaluate between options and make informed decisions on which will be more profitable in the long run. As a result, this standard relies on an understanding of probabilities as well as the expected means formula. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
In this equation the variables are identified as the following:
We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle owner's engine size with its respective probability and solve.
Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:
Round to the nearest one's place.
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Now, lets use this information to solve the problem. We will use the expected means formula and substitute the variable for the expected amount of money to be paid in the long run for each insurance policy given the probability of a minor and major accident. Let's start by calculating the expected expense associated with a high deductible insurance policy. Let's start by figuring out the expense for both the major and minor accidents associated with a high deductible policy. For the minor accident, the amount of the damage is less than the deductible; therefore, the entire amount must be paid by the motorist. Conversely, on the major accident, the motorist only needs to pay the complete deductible; therefore, we can write the following formula:
Substitute in our known values.
Solve.
Now, we need to add in the total cost of the policy for the year by adding in the sum of the monthly payments of the policy in a given year.
Next, we need to calculate the expected expense associated with a low deductible insurance policy. Let's start by figuring out the expense for both the major and minor accidents associated with a low deductible policy. For the minor accident, the amount of the damage is more than the deductible; therefore, the motorist only pays the low deductible. Likewise, on the major accident, the motorist only needs to pay the deductible; therefore, we can write the following formula:
Substitute in our known values.
Solve.
Now, we need to add in the total cost of the policy for the year by adding in the sum of the monthly payments of the policy in a given year.
Last, we need to subtract the expected expense of the high deductible policy from the lower one in order to calculate how much cheaper the lower deductible policy is.
The correct choice is the following:
The low deductible policy is cheaper by
Example Question #401 : High School: Statistics & Probability
A motorist is attempting to decide between the following two insurance policies:
A deductible is the amount of money that you have to pay out-of-pocket before your insurance company will cover the rest. In other words, if the total cost of an accident is and you have a deductible, then you will pay for the accident and your insurance will cover the remaining .
Consider the following:
Given this information which policy can we expect will save the motorist the most money in the following year?
The high deductible policy is cheaper by
The low deductible policy is cheaper by
The low deductible policy is cheaper by
The high deductible policy is cheaper by
Cannot be determined
The low deductible policy is cheaper by
This substandard specifically relates to strategies that can be used to evaluate and compare strategies associated with expected values. This means that we will use our knowledge of probabilities and expected values to evaluate between options and make informed decisions on which will be more profitable in the long run. As a result, this standard relies on an understanding of probabilities as well as the expected means formula. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
In this equation the variables are identified as the following:
We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle owner's engine size with its respective probability and solve.
Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:
Round to the nearest one's place.
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Now, lets use this information to solve the problem. We will use the expected means formula and substitute the variable for the expected amount of money to be paid in the long run for each insurance policy given the probability of a minor and major accident. Let's start by calculating the expected expense associated with a high deductible insurance policy. Let's start by figuring out the expense for both the major and minor accidents associated with a high deductible policy. For the minor accident, the amount of the damage is less than the deductible; therefore, the entire amount must be paid by the motorist. Conversely, on the major accident, the motorist only needs to pay the complete deductible; therefore, we can write the following formula:
Substitute in our known values.
Solve.
Now, we need to add in the total cost of the policy for the year by adding in the sum of the monthly payments of the policy in a given year.
Next, we need to calculate the expected expense associated with a low deductible insurance policy. Let's start by figuring out the expense for both the major and minor accidents associated with a low deductible policy. For the minor accident, the amount of the damage is more than the deductible; therefore, the motorist only pays the low deductible. Likewise, on the major accident, the motorist only needs to pay the deductible; therefore, we can write the following formula:
Substitute in our known values.
Solve.
Now, we need to add in the total cost of the policy for the year by adding in the sum of the monthly payments of the policy in a given year.
Last, we need to subtract the expected expense of the high deductible policy from the lower one in order to calculate how much cheaper the lower deductible policy is.
The correct choice is the following:
The low deductible policy is cheaper by
Example Question #402 : High School: Statistics & Probability
A motorist is attempting to decide between the following two insurance policies:
A deductible is the amount of money that you have to pay out-of-pocket before your insurance company will cover the rest. In other words, if the total cost of an accident is and you have a deductible, then you will pay for the accident and your insurance will cover the remaining .
Consider the following:
Given this information which policy can we expect will save the motorist the most money in the following year?
The high deductible policy is cheaper by
The low deductible policy is cheaper by
Cannot be determined
The high deductible policy is cheaper by
The low deductible policy is cheaper by
The low deductible policy is cheaper by
This substandard specifically relates to strategies that can be used to evaluate and compare strategies associated with expected values. This means that we will use our knowledge of probabilities and expected values to evaluate between options and make informed decisions on which will be more profitable in the long run. As a result, this standard relies on an understanding of probabilities as well as the expected means formula. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
In this equation the variables are identified as the following:
We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle owner's engine size with its respective probability and solve.
Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:
Round to the nearest one's place.
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Now, lets use this information to solve the problem. We will use the expected means formula and substitute the variable for the expected amount of money to be paid in the long run for each insurance policy given the probability of a minor and major accident. Let's start by calculating the expected expense associated with a high deductible insurance policy. Let's start by figuring out the expense for both the major and minor accidents associated with a high deductible policy. For the minor accident, the amount of the damage is less than the deductible; therefore, the entire amount must be paid by the motorist. Conversely, on the major accident, the motorist only needs to pay the complete deductible; therefore, we can write the following formula:
Substitute in our known values.
Solve.
Now, we need to add in the total cost of the policy for the year by adding in the sum of the monthly payments of the policy in a given year.
Next, we need to calculate the expected expense associated with a low deductible insurance policy. Let's start by figuring out the expense for both the major and minor accidents associated with a low deductible policy. For the minor accident, the amount of the damage is more than the deductible; therefore, the motorist only pays the low deductible. Likewise, on the major accident, the motorist only needs to pay the deductible; therefore, we can write the following formula:
Substitute in our known values.
Solve.
Now, we need to add in the total cost of the policy for the year by adding in the sum of the monthly payments of the policy in a given year.
Last, we need to subtract the expected expense of the high deductible policy from the lower one in order to calculate how much cheaper the lower deductible policy is.
The correct choice is the following:
The low deductible policy is cheaper by
Example Question #403 : High School: Statistics & Probability
A motorist is attempting to decide between the following two insurance policies:
A deductible is the amount of money that you have to pay out-of-pocket before your insurance company will cover the rest. In other words, if the total cost of an accident is and you have a deductible, then you will pay for the accident and your insurance will cover the remaining .
Consider the following:
Given this information which policy can we expect will save the motorist the most money in the following year?
The high deductible policy is cheaper by
Cannot be determined
The low deductible policy is cheaper by
The high deductible policy is cheaper by
The low deductible policy is cheaper by
The low deductible policy is cheaper by
This substandard specifically relates to strategies that can be used to evaluate and compare strategies associated with expected values. This means that we will use our knowledge of probabilities and expected values to evaluate between options and make informed decisions on which will be more profitable in the long run. As a result, this standard relies on an understanding of probabilities as well as the expected means formula. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
In this equation the variables are identified as the following:
We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle owner's engine size with its respective probability and solve.
Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:
Round to the nearest one's place.
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Now, lets use this information to solve the problem. We will use the expected means formula and substitute the variable for the expected amount of money to be paid in the long run for each insurance policy given the probability of a minor and major accident. Let's start by calculating the expected expense associated with a high deductible insurance policy. Let's start by figuring out the expense for both the major and minor accidents associated with a high deductible policy. For the minor accident, the amount of the damage is less than the deductible; therefore, the entire amount must be paid by the motorist. Conversely, on the major accident, the motorist only needs to pay the complete deductible; therefore, we can write the following formula:
Substitute in our known values.
Solve.
Now, we need to add in the total cost of the policy for the year by adding in the sum of the monthly payments of the policy in a given year.
Next, we need to calculate the expected expense associated with a low deductible insurance policy. Let's start by figuring out the expense for both the major and minor accidents associated with a low deductible policy. For the minor accident, the amount of the damage is more than the deductible; therefore, the motorist only pays the low deductible. Likewise, on the major accident, the motorist only needs to pay the deductible; therefore, we can write the following formula:
Substitute in our known values.
Solve.
Now, we need to add in the total cost of the policy for the year by adding in the sum of the monthly payments of the policy in a given year.
Last, we need to subtract the expected expense of the high deductible policy from the lower one in order to calculate how much cheaper the lower deductible policy is.
The correct choice is the following:
The low deductible policy is cheaper by
All Common Core: High School - Statistics and Probability Resources