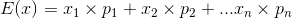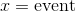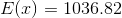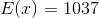All Common Core: High School - Statistics and Probability Resources
Example Questions
Example Question #1 : Possible Outcomes By Assigning Probabilities Vs. Finding Expected Values: Ccss.Math.Content.Hss Md.B.5
An unfair four-sided die is thrown and allowed to land without interruption. The probability and payoff of each side of the die is listed in the provided table.
The game costs 
None of these
Yes, because over the long run the cost of playing the game is greater than the expected payoff.
No, because over the long run the cost of playing the game is less than the expected payoff.
Yes, because over the long run the cost of playing the game is less than the expected payoff.
No, because over the long run the cost of playing the game is greater than the expected payoff.
Yes, because over the long run the cost of playing the game is less than the expected payoff.
This standard requires you to weigh the possible outcomes of a decision by assigning probabilities to payoff values and calculating the values of expected payoffs. In other words, this standard requires us to use the expected means equation to calculate the expected outcomes of a given game and decide if the game should or should not be played. This means that we must have a firm grasp on calculating probabilities as well as expected means. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
In this equation the variables are identified as the following:
We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle owner's engine size with its respective probability and solve.
Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:
Round to the nearest one's place.
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Now, lets use this information to solve the problem. We will use the expected means formula and substitute the 
Simplify.
The expected value of the payoff over the long run is less than the money needed to play: therefore, we can write the following:
The correct choice is "Yes, because over the long run the cost of playing the game is less than the expected payoff."
Example Question #2 : Possible Outcomes By Assigning Probabilities Vs. Finding Expected Values: Ccss.Math.Content.Hss Md.B.5
An unfair four-sided die is thrown and allowed to land without interruption. The probability and payoff of each side of the die is listed in the provided table.
The game costs 
No, because over the long run the cost of playing the game is less than the expected payoff.
No, because over the long run the cost of playing the game is greater than the expected payoff.
Yes, because over the long run the cost of playing the game is greater than the expected payoff.
None of these
Yes, because over the long run the cost of playing the game is less than the expected payoff.
No, because over the long run the cost of playing the game is greater than the expected payoff.
This standard requires you to weigh the possible outcomes of a decision by assigning probabilities to payoff values and calculating the values of expected payoffs. In other words, this standard requires us to use the expected means equation to calculate the expected outcomes of a given game and decide if the game should or should not be played. This means that we must have a firm grasp on calculating probabilities as well as expected means. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
In this equation the variables are identified as the following:
We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle owner's engine size with its respective probability and solve.
Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:
Round to the nearest one's place.
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Now, lets use this information to solve the problem. We will use the expected means formula and substitute the 
Simplify.
The expected value of the payoff over the long run is greater than the money needed to play: therefore, we can write the following:
The correct choice is "No, because over the long run the cost of playing the game is greater than the expected payoff."
Example Question #11 : Possible Outcomes By Assigning Probabilities Vs. Finding Expected Values: Ccss.Math.Content.Hss Md.B.5
An unfair four-sided die is thrown and allowed to land without interruption. The probability and payoff of each side of the die is listed in the provided table.
The game costs 
None of these
No, because over the long run the cost of playing the game is less than the expected payoff.
No, because over the long run the cost of playing the game is greater than the expected payoff.
Yes, because over the long run the cost of playing the game is less than the expected payoff.
Yes, because over the long run the cost of playing the game is greater than the expected payoff.
No, because over the long run the cost of playing the game is greater than the expected payoff.
This standard requires you to weigh the possible outcomes of a decision by assigning probabilities to payoff values and calculating the values of expected payoffs. In other words, this standard requires us to use the expected means equation to calculate the expected outcomes of a given game and decide if the game should or should not be played. This means that we must have a firm grasp on calculating probabilities as well as expected means. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
In this equation the variables are identified as the following:
We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle owner's engine size with its respective probability and solve.
Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:
Round to the nearest one's place.
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Now, lets use this information to solve the problem. We will use the expected means formula and substitute the 
Simplify.
The expected value of the payoff over the long run is greater than the money needed to play: therefore, we can write the following:
The correct choice is "No, because over the long run the cost of playing the game is greater than the expected payoff."
Example Question #12 : Possible Outcomes By Assigning Probabilities Vs. Finding Expected Values: Ccss.Math.Content.Hss Md.B.5
An unfair four-sided die is thrown and allowed to land without interruption. The probability and payoff of each side of the die is listed in the provided table.
The game costs 
Yes, because over the long run the cost of playing the game is greater than the expected payoff.
Yes, because over the long run the cost of playing the game is less than the expected payoff.
No, because over the long run the cost of playing the game is greater than the expected payoff.
No, because over the long run the cost of playing the game is less than the expected payoff.
None of these
Yes, because over the long run the cost of playing the game is less than the expected payoff.
This standard requires you to weigh the possible outcomes of a decision by assigning probabilities to payoff values and calculating the values of expected payoffs. In other words, this standard requires us to use the expected means equation to calculate the expected outcomes of a given game and decide if the game should or should not be played. This means that we must have a firm grasp on calculating probabilities as well as expected means. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
In this equation the variables are identified as the following:
We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle owner's engine size with its respective probability and solve.
Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:
Round to the nearest one's place.
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Now, lets use this information to solve the problem. We will use the expected means formula and substitute the 
Simplify.
The expected value of the payoff over the long run is greater than the money needed to play: therefore, we can write the following:
The correct choice is "Yes, because over the long run the cost of playing the game is less than the expected payoff."
Example Question #13 : Possible Outcomes By Assigning Probabilities Vs. Finding Expected Values: Ccss.Math.Content.Hss Md.B.5
An unfair four-sided die is thrown and allowed to land without interruption. The probability and payoff of each side of the die is listed in the provided table.
The game costs 
Yes, because over the long run the cost of playing the game is less than the expected payoff.
No, because over the long run the cost of playing the game is less than the expected payoff.
None of these
Yes, because over the long run the cost of playing the game is greater than the expected payoff.
No, because over the long run the cost of playing the game is greater than the expected payoff.
Yes, because over the long run the cost of playing the game is less than the expected payoff.
This standard requires you to weigh the possible outcomes of a decision by assigning probabilities to payoff values and calculating the values of expected payoffs. In other words, this standard requires us to use the expected means equation to calculate the expected outcomes of a given game and decide if the game should or should not be played. This means that we must have a firm grasp on calculating probabilities as well as expected means. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
In this equation the variables are identified as the following:
We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle owner's engine size with its respective probability and solve.
Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:
Round to the nearest one's place.
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Now, lets use this information to solve the problem. We will use the expected means formula and substitute the 
Simplify.
The expected value of the payoff over the long run is greater than the money needed to play: therefore, we can write the following:
The correct choice is "Yes, because over the long run the cost of playing the game is less than the expected payoff."
Example Question #1 : Expected Payoff For A Game Of Chance: Ccss.Math.Content.Hss Md.B.5a
The Witches' Duel is a game of chance. On each turn, there are four possible outcomes:
You earn 1 point with probability .2, and you lose 1 point with probability .3.
You earn 5 points with probability .35, and you lose 5 points with probability .15.
On average, how many points do you earn on each turn?
0.9 points
3.5 points
1.4 points
3.2 points
2.1 points
0.9 points
Example Question #52 : Using Probability To Make Decisions
A state lottery is holding a million dollar raffle and each ticket has the following odds of being a winner:
Which of the following choices best represents the price where tickets would start costing too much to play and expect to make money over the long run?
This substandard specifically relates to calculating the expected payoff of a game of chance (e.g. the expected winnings from a state lottery or a game at a fast-food restaurant). In this standard, you will be asked to calculate the expected value of a payoff of a game in order to determine whether or not it is worth playing. In this manner, students’ will learn how probabilities can inform their decisions to enhance winnings or avoid losses at games of chance. This standard relies on an understanding of probabilities as well as the expected means formula. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
In this equation the variables are identified as the following:
We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle owner's engine size with its respective probability and solve.
Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:
Round to the nearest one's place.
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Now, lets use this information to solve the problem. We are told that the payoff for the raffle is one million dollars and we know that each ticket has the following chances of being a winner:
We will use the expected means formula and substitute the 
Simplify.
Solve.
In the long run, the expected payoff is eight dollars. In other words, if we were to buy all the tickets we would break even at one million dollars if each only cost eight dollars. If the tickets cost more than this number, then it is not worth it to purchase a ticket when we associate this with the expected payoff. We need to choose the answer that is directly greater than eight dollars; therefore, the following choice is correct:
Example Question #51 : Using Probability To Make Decisions
Ernie has three bets to choose from.
Bet 1 will cost him $10, Bet 2 will cost him $15, and Bet 3 will cost him $20.
The payout probabilities are as follows:
Which bet should Ernie pick?
Bet 1
Bet 2
Ernie shouldn't take any of the three bets because he's expected to lose money on all of them.
Bet 3
Ernie shouldn't take any of the three bets because he's expected to lose money on all of them.
Example Question #2 : Evaluate And Compare Strategies Of Expected Values: Ccss.Math.Content.Hss Md.B.5b
A motorist is attempting to decide between the following two insurance policies:

A deductible is the amount of money that you have to pay out-of-pocket before your insurance company will cover the rest. In other words, if the total cost of an accident is 



Consider the following:

Given this information which policy can we expect will save the motorist the most money in the following year?
The low deductible policy is cheaper by
The high deductible policy is cheaper by
The low deductible policy is cheaper by
The high deductible policy is cheaper by
Cannot be determined
The high deductible policy is cheaper by
This substandard specifically relates to strategies that can be used to evaluate and compare strategies associated with expected values. This means that we will use our knowledge of probabilities and expected values to evaluate between options and make informed decisions on which will be more profitable in the long run. As a result, this standard relies on an understanding of probabilities as well as the expected means formula. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
In this equation the variables are identified as the following:
We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle owner's engine size with its respective probability and solve.
Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:
Round to the nearest one's place.
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Now, lets use this information to solve the problem. We will use the expected means formula and substitute the 
Substitute in our known values.
Solve.
Now, we need to add in the total cost of the policy for the year by adding in the sum of the monthly payments of the policy in a given year.
Next, we need to calculate the expected expense associated with a low deductible insurance policy. Let's start by figuring out the expense for both the major and minor accidents associated with a low deductible policy. For the minor accident, the amount of the damage is more than the deductible; therefore, the motorist only pays the low deductible. Likewise, on the major accident, the motorist only needs to pay the deductible; therefore, we can write the following formula:
Substitute in our known values.
Solve.
Now, we need to add in the total cost of the policy for the year by adding in the sum of the monthly payments of the policy in a given year.
Last, we need to subtract the expected expense of the low deductible policy from the higher one in order to calculate how much cheaper the higher deductible policy is.
The correct choice is the following:
The high deductible policy is cheaper by
Example Question #3 : Evaluate And Compare Strategies Of Expected Values: Ccss.Math.Content.Hss Md.B.5b
A motorist is attempting to decide between the following two insurance policies:

A deductible is the amount of money that you have to pay out-of-pocket before your insurance company will cover the rest. In other words, if the total cost of an accident is 



Consider the following:

Given this information which policy can we expect will save the motorist the most money in the following year?
The high deductible policy is cheaper by
The low deductible policy is cheaper by
Cannot be determined
The low deductible policy is cheaper by
The high deductible policy is cheaper by
The high deductible policy is cheaper by
This substandard specifically relates to strategies that can be used to evaluate and compare strategies associated with expected values. This means that we will use our knowledge of probabilities and expected values to evaluate between options and make informed decisions on which will be more profitable in the long run. As a result, this standard relies on an understanding of probabilities as well as the expected means formula. First, we will discuss probabilities in a general sense.
A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
According to this logic, we would expect to roll a particular number on a die one out of every six rolls; however, we may roll the same number multiple times or not at all in six rolls. This discrepancy creates a difference between the expected mean and the actual mean. The expected mean is a hypothetical calculation that assumes a very large sample size and no intervening variables (such as differing forces on the roll and changes in the friction of the surface the die is rolled upon between rolls). Under these conditions we can calculate that any number on the die in a "perfect world" should be one out of six. On the other hand the true or actual mean is calculated using "real" date. In these calculations we would roll a die a particular number of times and use it to develop a probability of rolling a particular number. It is important to note that, theoretically, actual means will eventually equal expected means over a large—or near infinite—amount of trials. In other words, over many many rolls we would eventually find that each number on the die has a one in six chance of being rolled.
Now, let's discuss how expected means are determined. The expected mean is calculated using the following formula:
In this equation the variables are identified as the following:
We can illustrate this using an example problem. A list of individuals and the respective size of their motorcycles in cubic inches is provided. If you were to randomly select any one person from the list, then what size would you expect their motorcycle to be?

Let's use this information to solve the problem. In order to solve the motorcycle problem, we need to use the expected mean formula. We will substitute each of the motorcycle owner's engine size with its respective probability and solve.
Each of the values have the same probability of being chosen—one out of eleven. As a result, we can simplify this equation:
Round to the nearest one's place.
Note that we can solve this problem in this simplified manner because all of the people had an equal probability of being chosen. If his or her probabilities differed, then we would need to substitute in each person’s respective probability of being chosen.
Now, lets use this information to solve the problem. We will use the expected means formula and substitute the 
Substitute in our known values.
Solve.
Now, we need to add in the total cost of the policy for the year by adding in the sum of the monthly payments of the policy in a given year.
Next, we need to calculate the expected expense associated with a low deductible insurance policy. Let's start by figuring out the expense for both the major and minor accidents associated with a low deductible policy. For the minor accident, the amount of the damage is more than the deductible; therefore, the motorist only pays the low deductible. Likewise, on the major accident, the motorist only needs to pay the deductible; therefore, we can write the following formula:
Substitute in our known values.
Solve.
Now, we need to add in the total cost of the policy for the year by adding in the sum of the monthly payments of the policy in a given year.
Last, we need to subtract the expected expense of the low deductible policy from the higher one in order to calculate how much cheaper the higher deductible policy is.
The correct choice is the following:
The high deductible policy is cheaper by
Certified Tutor
Certified Tutor
All Common Core: High School - Statistics and Probability Resources