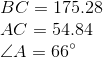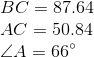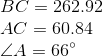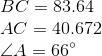Call Now to Set Up Tutoring:

(888) 888-0446

Common Core: High School - Geometry : Apply Laws of Sines and Cosines: CCSS.Math.Content.HSG-SRT.D.11

Study concepts, example questions & explanations for Common Core: High School - Geometry

Create An Account

All Common Core: High School - Geometry Resources

6 Diagnostic Tests 114 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #11 : Apply Laws Of Sines And Cosines: Ccss.Math.Content.Hsg Srt.D.11

In a triangle where the side opposite a $26 ^{\circ}$ has length 11 find the side opposite a $17 ^{\circ}$ angle. Round you answer to the nearest hundredth.

Possible Answers:

0.37

2.71

4.06

0.25

44.63

Correct answer:

2.71

Explanation:

In order to solve this, we need to recall the law of sines.

$\frac{1}{A} \sin{\left (a \right )} = \frac{1}{B} \sin{\left (b \right )}$

Where , and are angles, and , and , are opposite side lengths.

Now let's plug in 26 for , 11 for and 17 for .
Now our equation becomes

$\left(\frac{\sin( 26 )}{ 11 }\right)= \left(\frac{\sin( 17 )}{ b }\right)$

Now we rearrange the equation to solve for b

$\\b = \left(\frac{ 11 \sin( 17 )}{\sin( 26 )}\right) \\\\b = 2.71142149312156$

Now we round our answer to the nearest tenth.

b = 2.71

Remember if your answer is negative, multiply it by -1, because side lengths can't be negative.

Report an Error

Example Question #12 : Apply Laws Of Sines And Cosines: Ccss.Math.Content.Hsg Srt.D.11

In a triangle where the side opposite a $81 ^{\circ}$ has length 11 find the side opposite a $66 ^{\circ}$ angle. Round you answer to the nearest hundredth.

Possible Answers:

9.90

0.08

0.90

12.23

1.11

Correct answer:

12.23

Explanation:

In order to solve this, we need to recall the law of sines.

$\frac{1}{A} \sin{\left (a \right )} = \frac{1}{B} \sin{\left (b \right )}$

Where , and are angles, and , and , are opposite side lengths.

Now let's plug in 81 for , 11 for and 66 for .
Now our equation becomes

$\left(\frac{\sin( 81 )}{ 11 }\right)= \left(\frac{\sin( 66 )}{ b }\right)$

Now we rearrange the equation to solve for b

$\\b = \left(\frac{ 11 \sin( 66 )}{\sin( 81 )}\right) \\\\b = 12.2250984628794$

Now we round our answer to the nearest tenth.

b = 12.23

Remember if your answer is negative, multiply it by -1, because side lengths can't be negative.

Report an Error

Example Question #13 : Apply Laws Of Sines And Cosines: Ccss.Math.Content.Hsg Srt.D.11

In a triangle where the side opposite a $70 ^{\circ}$ has length 5 find the side opposite a $50 ^{\circ}$ angle. Round you answer to the nearest hundredth.

Possible Answers:

0.53

2.66

13.29

0.38

1.88

Correct answer:

1.88

Explanation:

In order to solve this, we need to recall the law of sines.

$\frac{1}{A} \sin{\left (a \right )} = \frac{1}{B} \sin{\left (b \right )}$

Where , and are angles, and , and , are opposite side lengths.

Now let's plug in 70 for , 5 for and 50 for .
Now our equation becomes

$\left(\frac{\sin( 70 )}{ 5 }\right)= \left(\frac{\sin( 50 )}{ b }\right)$

Now we rearrange the equation to solve for b

$\\b = \left(\frac{ 5 \sin( 50 )}{\sin( 70 )}\right) \\\\b = -1.88083767684263$

Now we round our answer to the nearest tenth.

b = -1.88

Remember if your answer is negative, multiply it by -1, because side lengths can't be negative.

b = 1.88

Report an Error

Example Question #14 : Apply Laws Of Sines And Cosines: Ccss.Math.Content.Hsg Srt.D.11

In a triangle where the side opposite a $11 ^{\circ}$ has length 5 find the side opposite a $64 ^{\circ}$ angle. Round you answer to the nearest hundredth.

Possible Answers:

0.29

1.47

0.68

3.41

7.33

Correct answer:

3.41

Explanation:

In order to solve this, we need to recall the law of sines.

$\frac{1}{A} \sin{\left (a \right )} = \frac{1}{B} \sin{\left (b \right )}$

Where , and are angles, and , and , are opposite side lengths.

Now let's plug in 11 for , 5 for and 64 for .
Now our equation becomes

$\left(\frac{\sin( 11 )}{ 5 }\right)= \left(\frac{\sin( 64 )}{ b }\right)$

Now we rearrange the equation to solve for b

$\\b = \left(\frac{ 5 \sin( 64 )}{\sin( 11 )}\right) \\\\b = -3.41136278039312$

Now we round our answer to the nearest tenth.

b = -3.41

Remember if your answer is negative, multiply it by -1, because side lengths can't be negative.

b = 3.41

Report an Error

Example Question #11 : Apply Laws Of Sines And Cosines: Ccss.Math.Content.Hsg Srt.D.11

In a triangle where the side opposite a $78 ^{\circ}$ has length 6 find the side opposite a $52 ^{\circ}$ angle. Round you answer to the nearest hundredth.

Possible Answers:

1.08

6.49

5.54

0.18

0.92

Correct answer:

5.54

Explanation:

In order to solve this, we need to recall the law of sines.

$\frac{1}{A} \sin{\left (a \right )} = \frac{1}{B} \sin{\left (b \right )}$

Where , and are angles, and , and , are opposite side lengths.

Now let's plug in 78 for , 6 for and 52 for .
Now our equation becomes

$\left(\frac{\sin( 78 )}{ 6 }\right)= \left(\frac{\sin( 52 )}{ b }\right)$

Now we rearrange the equation to solve for b

$\\b = \left(\frac{ 6 \sin( 52 )}{\sin( 78 )}\right) \\\\b = 5.54498774628774$

Now we round our answer to the nearest tenth.

b = 5.54

Remember if your answer is negative, multiply it by -1, because side lengths can't be negative.

Report an Error

Example Question #16 : Apply Laws Of Sines And Cosines: Ccss.Math.Content.Hsg Srt.D.11

In a triangle where the side opposite a $44 ^{\circ}$ has length 7 find the side opposite a $53 ^{\circ}$ angle. Round you answer to the nearest hundredth.

Possible Answers:

6.67

0.15

0.95

1.05

7.34

Correct answer:

6.67

Explanation:

In order to solve this, we need to recall the law of sines.

$\frac{1}{A} \sin{\left (a \right )} = \frac{1}{B} \sin{\left (b \right )}$

Where , and are angles, and , and , are opposite side lengths.

Now let's plug in 44 for , 7 for and 53 for .
Now our equation becomes

$\left(\frac{\sin( 44 )}{ 7 }\right)= \left(\frac{\sin( 53 )}{ b }\right)$

Now we rearrange the equation to solve for b

$\\b = \left(\frac{ 7 \sin( 53 )}{\sin( 44 )}\right) \\\\b = 6.67220075275393$

Now we round our answer to the nearest tenth.

b = 6.67

Remember if your answer is negative, multiply it by -1, because side lengths can't be negative.

Report an Error

Example Question #11 : Apply Laws Of Sines And Cosines: Ccss.Math.Content.Hsg Srt.D.11

To the nearest hundredth, solve $\bigtriangleup ABC$ where, AB = 179 , $\angle B= 11 ^{\circ}$ , and $\angle C= 71 ^{\circ}$ .

Possible Answers:

$\\BC = 183.47 \\AC = 28.896 \\\angle A = 98^\circ$

$\\BC = 562.41 \\AC = 46.12 \\\angle A = 98^\circ$

$\\BC = 187.47 \\AC = 36.12 \\\angle A = 98^\circ$

$\\BC = 190.47 \\AC = 10.836 \\\angle A = 98^\circ$

$\\BC = 374.94 \\AC = 40.12 \\\angle A = 98^\circ$

Correct answer:

$\\BC = 187.47 \\AC = 36.12 \\\angle A = 98^\circ$

Explanation:

The first step is to create a picture

Plot1

Since we have 2 angles, we can solve for the 3rd angle easily.

$\\\angle A =180- 11 - 71 \\\angle A = 98^\circ$

Now we can use the Law of Sines to figure out one side

Recall the Law of Sines

$\frac{1}{a} \sin{\left (A \right )} = \frac{1}{AC} \sin{\left (B \right )}$

Now plug in 11 for B , 71 for A and 179 for a , and solve for the missing side.

$\\\left(\frac{\sin( 71 )}{ 179 }\right)= \left(\frac{\sin( 11 )}{ AC }\right) \\\\AC = \left(\frac{ 179 \sin( 11 )}{\sin( 71 )}\right) \\\\AC = 36.1228336003367$

Remember to round to the nearest hundredth.

AC = 36.12

Now we need to solve for the last side of the triangle.

To solve for this, we can use the Law of Cosines.

Lets recall the Law of Cosines.

$\\BC^{2} = a^{2} - 2 a b \cos{\left (BC \right )} + b^{2} \\BC^2 = 1304.6544 + 32041 - 2 \cdot 36.12 \cdot 179 \cdot \cos( 98 ) \\BC^{2} = 35145.2962015906 \\BC = 187.470787595269 \\BC = 187.47$

Report an Error

Example Question #12 : Apply Laws Of Sines And Cosines: Ccss.Math.Content.Hsg Srt.D.11

To the nearest hundredth, solve $\bigtriangleup ABC$ where, AB = 78 , $\angle B= 18 ^{\circ}$ , and $\angle C= 66 ^{\circ}$ .

Possible Answers:

$\\BC = 169.82 \\AC = 30.38 \\\angle A = 96^\circ$

$\\BC = 254.73 \\AC = 36.38 \\\angle A = 96^\circ$

$\\BC = 80.91 \\AC = 21.104 \\\angle A = 96^\circ$

$\\BC = 87.91 \\AC = 7.914 \\\angle A = 96^\circ$

$\\BC = 84.91 \\AC = 26.38 \\\angle A = 96^\circ$

Correct answer:

$\\BC = 84.91 \\AC = 26.38 \\\angle A = 96^\circ$

Explanation:

The first step is to create a picture

Plot2

Since we have 2 angles, we can solve for the 3rd angle easily.

$\\\angle A =180- 18 - 66 \\\angle A = 96^\circ$

Now we can use the Law of Sines to figure out one side

Recall the Law of Sines

$\frac{1}{a} \sin{\left (A \right )} = \frac{1}{AC} \sin{\left (B \right )}$

Now plug in 18 for B , 66 for A and 78 for a , and solve for the missing side.

$\\\left(\frac{\sin( 66 )}{ 78 }\right)= \left(\frac{\sin( 18 )}{ AC }\right) \\\\AC = \left(\frac{ 78 \sin( 18 )}{\sin( 66 )}\right) \\\\AC = 26.3843745919819$

Remember to round to the nearest hundredth.

AC = 26.38

Now we need to solve for the last side of the triangle.

To solve for this, we can use the Law of Cosines.

Lets recall the Law of Cosines.

$\\BC^{2} = a^{2} - 2 a b \cos{\left (BC \right )} + b^{2} \\BC^2 = 695.9043999999999 + 6084 - 2 \cdot 26.38 \cdot 78 \cdot \cos( 96 ) \\BC^{2} = 7210.06829431611 \\BC = 84.9121210094066 \\BC = 84.91$

Report an Error

Example Question #12 : Apply Laws Of Sines And Cosines: Ccss.Math.Content.Hsg Srt.D.11

To the nearest hundredth, solve $\bigtriangleup ABC$ where, AB = 95 , $\angle B= 32 ^{\circ}$ , and $\angle C= 82 ^{\circ}$ .

Possible Answers:

$\\BC = 87.64 \\AC = 50.84 \\\angle A = 66^\circ$

$\\BC = 83.64 \\AC = 40.672 \\\angle A = 66^\circ$

$\\BC = 90.64 \\AC = 15.252 \\\angle A = 66^\circ$

$\\BC = 175.28 \\AC = 54.84 \\\angle A = 66^\circ$

$\\BC = 262.92 \\AC = 60.84 \\\angle A = 66^\circ$

Correct answer:

$\\BC = 87.64 \\AC = 50.84 \\\angle A = 66^\circ$

Explanation:

The first step is to create a picture

Plot3

Since we have 2 angles, we can solve for the 3rd angle easily.

$\\\angle A =180- 32 - 82 \\\angle A = 66^\circ$

Now we can use the Law of Sines to figure out one side

Recall the Law of Sines

$\frac{1}{a} \sin{\left (A \right )} = \frac{1}{AC} \sin{\left (B \right )}$

Now plug in 32 for B , 82 for A and 95 for a , and solve for the missing side.

$\\\left(\frac{\sin( 82 )}{ 95 }\right)= \left(\frac{\sin( 32 )}{ AC }\right) \\\\AC = \left(\frac{ 95 \sin( 32 )}{\sin( 82 )}\right) \\\\AC = 50.8370730019896$

Remember to round to the nearest hundredth.

AC = 50.84

Now we need to solve for the last side of the triangle.

To solve for this, we can use the Law of Cosines.

Lets recall the Law of Cosines.

$\\BC^{2} = a^{2} - 2 a b \cos{\left (BC \right )} + b^{2} \\BC^2 = 2584.7056000000002 + 9025 - 2 \cdot 50.84 \cdot 95 \cdot \cos( 66 ) \\BC^{2} = 7680.792322545 \\BC = 87.6401296356013 \\BC = 87.64$

Report an Error

Example Question #14 : Apply Laws Of Sines And Cosines: Ccss.Math.Content.Hsg Srt.D.11

To the nearest hundredth, solve $\bigtriangleup ABC$ where, AB = 182 , $\angle B= 3 ^{\circ}$ , and $\angle C= 81 ^{\circ}$ .

Possible Answers:

$\\BC = 366.52 \\AC = 13.64 \\\angle A = 96^\circ$

$\\BC = 183.26 \\AC = 9.64 \\\angle A = 96^\circ$

$\\BC = 549.78 \\AC = 19.64 \\\angle A = 96^\circ$

$\\BC = 186.26 \\AC = 2.892 \\\angle A = 96^\circ$

$\\BC = 179.26 \\AC = 7.712 \\\angle A = 96^\circ$

Correct answer:

$\\BC = 183.26 \\AC = 9.64 \\\angle A = 96^\circ$

Explanation:

The first step is to create a picture

Plot4

Since we have 2 angles, we can solve for the 3rd angle easily.

$\\\angle A =180- 3 - 81 \\\angle A = 96^\circ$

Now we can use the Law of Sines to figure out one side

Recall the Law of Sines

$\frac{1}{a} \sin{\left (A \right )} = \frac{1}{AC} \sin{\left (B \right )}$

Now plug in 3 for B , 81 for A and 182 for a , and solve for the missing side.

$\\\left(\frac{\sin( 81 )}{ 182 }\right)= \left(\frac{\sin( 3 )}{ AC }\right) \\\\AC = \left(\frac{ 182 \sin( 3 )}{\sin( 81 )}\right) \\\\AC = 9.64387615477605$

Remember to round to the nearest hundredth.

AC = 9.64

Now we need to solve for the last side of the triangle.

To solve for this, we can use the Law of Cosines.

Lets recall the Law of Cosines.

$\\BC^{2} = a^{2} - 2 a b \cos{\left (BC \right )} + b^{2} \\BC^2 = 92.92960000000001 + 33124 - 2 \cdot 9.64 \cdot 182 \cdot \cos( 96 ) \\BC^{2} = 33583.7157964677 \\BC = 183.25860360831 \\BC = 183.26$

Report an Error

View Tutors

Keenia
Certified Tutor

Nova Southeastern University, Master of Science, Special Education. Nova Southeastern University, Master of Science, Educatio...

View Tutors

Brandon
Certified Tutor

University of Houston, Bachelor of Science, Biology, General. University of North Texas, Doctor of Philosophy, Pharmacy.

View Tutors

Adriana
Certified Tutor

Lone Star College System, Associate in Arts, Arts, General. University of Houston, Bachelor in Arts, Business Administration ...

All Common Core: High School - Geometry Resources

6 Diagnostic Tests 114 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in San Diego, ACT Tutors in Denver, Algebra Tutors in Boston, Reading Tutors in Dallas Fort Worth, Spanish Tutors in San Francisco-Bay Area, GMAT Tutors in Los Angeles, GRE Tutors in Houston, SSAT Tutors in Los Angeles, Biology Tutors in Dallas Fort Worth, LSAT Tutors in New York City

Popular Courses & Classes

ACT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Atlanta, ISEE Courses & Classes in Chicago, SAT Courses & Classes in Denver, GMAT Courses & Classes in Phoenix, ACT Courses & Classes in Miami, GMAT Courses & Classes in Philadelphia, GMAT Courses & Classes in Los Angeles, ACT Courses & Classes in Dallas Fort Worth

Popular Test Prep

GMAT Test Prep in Phoenix, LSAT Test Prep in New York City, GRE Test Prep in Houston, ACT Test Prep in Dallas Fort Worth, ACT Test Prep in Miami, GMAT Test Prep in Los Angeles, GRE Test Prep in Dallas Fort Worth, SSAT Test Prep in Denver, GRE Test Prep in Seattle, SAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Common Core: High School - Geometry : Apply Laws of Sines and Cosines: CCSS.Math.Content.HSG-SRT.D.11

Study concepts, example questions & explanations for Common Core: High School - Geometry

All Common Core: High School - Geometry Resources

Example Questions

Example Question #11 : Apply Laws Of Sines And Cosines: Ccss.Math.Content.Hsg Srt.D.11

Example Question #12 : Apply Laws Of Sines And Cosines: Ccss.Math.Content.Hsg Srt.D.11

Example Question #13 : Apply Laws Of Sines And Cosines: Ccss.Math.Content.Hsg Srt.D.11

Example Question #14 : Apply Laws Of Sines And Cosines: Ccss.Math.Content.Hsg Srt.D.11

Example Question #11 : Apply Laws Of Sines And Cosines: Ccss.Math.Content.Hsg Srt.D.11

Example Question #16 : Apply Laws Of Sines And Cosines: Ccss.Math.Content.Hsg Srt.D.11

Example Question #11 : Apply Laws Of Sines And Cosines: Ccss.Math.Content.Hsg Srt.D.11

Example Question #12 : Apply Laws Of Sines And Cosines: Ccss.Math.Content.Hsg Srt.D.11

Example Question #12 : Apply Laws Of Sines And Cosines: Ccss.Math.Content.Hsg Srt.D.11

Example Question #14 : Apply Laws Of Sines And Cosines: Ccss.Math.Content.Hsg Srt.D.11

All Common Core: High School - Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: