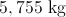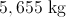All Common Core: 8th Grade Math Resources
Example Questions
Example Question #21 : Apply The Pythagorean Theorem To Find The Distance Between Two Points In A Coordinate System: Ccss.Math.Content.8.G.B.8
Use the Pythagorean Theorem to calculate the length of the line shown on the provided coordinate plane. Round the answer to the nearest tenth.

Notice that the diagonal line from the problem could be the hypotenuse of a right triangle. If we add two more lines, then we can create a closed figure in the shape of a triangle:

Let's use the Pythagorean Theorem to calculate the length of the line that represents the hypotenuse of a right triangle. The Pythagorean Theorem states that for right triangles:
In this equation:
We can count the number of units on the coordinate plane that were used to create the legs of our drawn triangle. Afterwards, we can use the Pythagorean Theorem to solve for the length of the hypotenuse, or the original diagonal line.
In order to solve for this problem we want to substitute in the known side lengths for the triangle's legs:
Example Question #22 : Apply The Pythagorean Theorem To Find The Distance Between Two Points In A Coordinate System: Ccss.Math.Content.8.G.B.8
Use the Pythagorean Theorem to calculate the length of the line shown on the provided coordinate plane. Round the answer to the nearest tenth.

Notice that the diagonal line from the problem could be the hypotenuse of a right triangle. If we add two more lines, then we can create a closed figure in the shape of a triangle:

Let's use the Pythagorean Theorem to calculate the length of the line that represents the hypotenuse of a right triangle. The Pythagorean Theorem states that for right triangles:
In this equation:
We can count the number of units on the coordinate plane that were used to create the legs of our drawn triangle. Afterwards, we can use the Pythagorean Theorem to solve for the length of the hypotenuse, or the original diagonal line.
In order to solve for this problem we want to substitute in the known side lengths for the triangle's legs:
Example Question #23 : Apply The Pythagorean Theorem To Find The Distance Between Two Points In A Coordinate System: Ccss.Math.Content.8.G.B.8
Use the Pythagorean Theorem to calculate the length of the line shown on the provided coordinate plane. Round the answer to the nearest tenth.

Notice that the diagonal line from the problem could be the hypotenuse of a right triangle. If we add two more lines, then we can create a closed figure in the shape of a triangle:

Let's use the Pythagorean Theorem to calculate the length of the line that represents the hypotenuse of a right triangle. The Pythagorean Theorem states that for right triangles:
In this equation:
We can count the number of units on the coordinate plane that were used to create the legs of our drawn triangle. Afterwards, we can use the Pythagorean Theorem to solve for the length of the hypotenuse, or the original diagonal line.
In order to solve for this problem we want to substitute in the known side lengths for the triangle's legs:
Example Question #24 : Apply The Pythagorean Theorem To Find The Distance Between Two Points In A Coordinate System: Ccss.Math.Content.8.G.B.8
Use the Pythagorean Theorem to calculate the length of the line shown on the provided coordinate plane. Round the answer to the nearest tenth.

Notice that the diagonal line from the problem could be the hypotenuse of a right triangle. If we add two more lines, then we can create a closed figure in the shape of a triangle:

Let's use the Pythagorean Theorem to calculate the length of the line that represents the hypotenuse of a right triangle. The Pythagorean Theorem states that for right triangles:
In this equation:
We can count the number of units on the coordinate plane that were used to create the legs of our drawn triangle. Afterwards, we can use the Pythagorean Theorem to solve for the length of the hypotenuse, or the original diagonal line.
In order to solve for this problem we want to substitute in the known side lengths for the triangle's legs:
Example Question #25 : Apply The Pythagorean Theorem To Find The Distance Between Two Points In A Coordinate System: Ccss.Math.Content.8.G.B.8
Use the Pythagorean Theorem to calculate the length of the line shown on the provided coordinate plane. Round the answer to the nearest tenth.

Notice that the diagonal line from the problem could be the hypotenuse of a right triangle. If we add two more lines, then we can create a closed figure in the shape of a triangle:

Let's use the Pythagorean Theorem to calculate the length of the line that represents the hypotenuse of a right triangle. The Pythagorean Theorem states that for right triangles:
In this equation:
We can count the number of units on the coordinate plane that were used to create the legs of our drawn triangle. Afterwards, we can use the Pythagorean Theorem to solve for the length of the hypotenuse, or the original diagonal line.
In order to solve for this problem we want to substitute in the known side lengths for the triangle's legs:
Example Question #26 : Apply The Pythagorean Theorem To Find The Distance Between Two Points In A Coordinate System: Ccss.Math.Content.8.G.B.8
Use the Pythagorean Theorem to calculate the length of the line shown on the provided coordinate plane. Round the answer to the nearest tenth.

Notice that the diagonal line from the problem could be the hypotenuse of a right triangle. If we add two more lines, then we can create a closed figure in the shape of a triangle:

Let's use the Pythagorean Theorem to calculate the length of the line that represents the hypotenuse of a right triangle. The Pythagorean Theorem states that for right triangles:
In this equation:
We can count the number of units on the coordinate plane that were used to create the legs of our drawn triangle. Afterwards, we can use the Pythagorean Theorem to solve for the length of the hypotenuse, or the original diagonal line.
In order to solve for this problem we want to substitute in the known side lengths for the triangle's legs:
Example Question #161 : Geometry
Use the Pythagorean Theorem to calculate the length of the line shown on the provided coordinate plane. Round the answer to the nearest tenth.

Notice that the diagonal line from the problem could be the hypotenuse of a right triangle. If we add two more lines, then we can create a closed figure in the shape of a triangle:

Let's use the Pythagorean Theorem to calculate the length of the line that represents the hypotenuse of a right triangle. The Pythagorean Theorem states that for right triangles:
In this equation:
We can count the number of units on the coordinate plane that were used to create the legs of our drawn triangle. Afterwards, we can use the Pythagorean Theorem to solve for the length of the hypotenuse, or the original diagonal line.
In order to solve for this problem we want to substitute in the known side lengths for the triangle's legs:
Example Question #21 : Apply The Pythagorean Theorem To Find The Distance Between Two Points In A Coordinate System: Ccss.Math.Content.8.G.B.8
Use the Pythagorean Theorem to calculate the length of the line shown on the provided coordinate plane. Round the answer to the nearest tenth.

Notice that the diagonal line from the problem could be the hypotenuse of a right triangle. If we add two more lines, then we can create a closed figure in the shape of a triangle:

Let's use the Pythagorean Theorem to calculate the length of the line that represents the hypotenuse of a right triangle. The Pythagorean Theorem states that for right triangles:
In this equation:
We can count the number of units on the coordinate plane that were used to create the legs of our drawn triangle. Afterwards, we can use the Pythagorean Theorem to solve for the length of the hypotenuse, or the original diagonal line.
In order to solve for this problem we want to substitute in the known side lengths for the triangle's legs:
Example Question #511 : Geometry
Susie walks north from her house to a park that is 30 meters away. Once she arrives at the park, she turns and walks west for 80 meters to a bench to feed some pigeons. She then walks north for another 30 meters to a concession stand. If Susie returns home in a straight line from the concession stand, how far will she walk from the concession stand to her house, in meters?
200
25
100
50
70
100
Susie walks 30 meters north, then 80 meters west, then 30 meters north again. Thus, she walks 60 meters north and 80 meters west. These two directions are 90 degrees away from one another.
At this point, construct a right triangle with one leg that measures 60 meters and a second leg that is 80 meters.
You can save time by using the 3:4:5 common triangle. 60 and 80 are 


We can solve for the length of the missing hypotenuse by applying the Pythagorean theorem:
Substitute the following known values into the formula and solve for the missing hypotenuse: side 
Susie will walk 100 meters to reach her house.
Example Question #621 : Geometry
Chestnut wood has a density of about 
First, convert the dimensions to cubic centimeters by multiplying by 


Its volume is found by using the formula and the converted height and radius.
Now multiply this by 
Finally, convert the answer to kilograms.
All Common Core: 8th Grade Math Resources