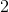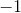All Common Core: 8th Grade Math Resources
Example Questions
Example Question #141 : Grade 8
Using the similar triangles, find the equation of the line in the provided graph.

The equation for a line can be written in the slope-intercept form:

In this equation, the variables 


One way to find the slope of a line is to solve for the rise over run:
This is defined as the change in the y-axis over the change in the x axis.
The triangles in the graph provide possess two different values for their respective rise over run calculations; however, both triangle should have the same slope:
Now that we've found the slope of our line, 
Therefore, the equation of this line is,
Example Question #141 : Grade 8
Using the similar triangles, find the equation of the line in the provided graph.

The equation for a line can be written in the slope-intercept form:

In this equation, the variables 


One way to find the slope of a line is to solve for the rise over run:
This is defined as the change in the y-axis over the change in the x axis.
The triangles in the graph provide possess two different values for their respective rise over run calculations; however, both triangle should have the same slope:
Now that we've found the slope of our line, 
Therefore, the equation of this line is,
Example Question #143 : Grade 8
Using the similar triangles, find the equation of the line in the provided graph.

The equation for a line can be written in the slope-intercept form:

In this equation, the variables 


One way to find the slope of a line is to solve for the rise over run:
This is defined as the change in the y-axis over the change in the x axis.
The triangles in the graph provide possess two different values for their respective rise over run calculations; however, both triangle should have the same slope:
Now that we've found the slope of our line, 
Therefore, the equation of this line is,
Example Question #142 : Grade 8
Using the similar triangles, find the equation of the line in the provided graph.

The equation for a line can be written in the slope-intercept form:

In this equation, the variables 


One way to find the slope of a line is to solve for the rise over run:
This is defined as the change in the y-axis over the change in the x axis.
The triangles in the graph provide possess two different values for their respective rise over run calculations; however, both triangle should have the same slope:
Now that we've found the slope of our line, 
Therefore, the equation of this line is,
Example Question #23 : Use Similar Triangles To Show Equal Slopes: Ccss.Math.Content.8.Ee.B.6
Using the similar triangles, find the equation of the line in the provided graph.

The equation for a line can be written in the slope-intercept form:

In this equation, the variables 


One way to find the slope of a line is to solve for the rise over run:
This is defined as the change in the y-axis over the change in the x axis.
The triangles in the graph provide possess two different values for their respective rise over run calculations; however, both triangle should have the same slope:
Now that we've found the slope of our line, 
Therefore, the equation of this line is,
Example Question #151 : Grade 8
Using the similar triangles, find the equation of the line in the provided graph.

The equation for a line can be written in the slope-intercept form:

In this equation, the variables 


One way to find the slope of a line is to solve for the rise over run:
This is defined as the change in the y-axis over the change in the x axis.
The triangles in the graph provide possess two different values for their respective rise over run calculations; however, both triangle should have the same slope:
Now that we've found the slope of our line, 
Therefore, the equation of this line is,
Example Question #1 : How To Find Out When An Equation Has No Solution
Solve the rational equation:

no solution
no solution
With rational equations we must first note the domain, which is all real numbers except 










Example Question #2 : How To Find Out When An Equation Has No Solution
How many solutions does the equation below have?
Two
Three
One
Infinite
No solutions
No solutions
When finding how many solutions an equation has you need to look at the constants and coefficients.
The coefficients are the numbers alongside the variables.
The constants are the numbers alone with no variables.
If the coefficients are the same on both sides then the sides will not equal, therefore no solutions will occur.
Use distributive property on the right side first.

No solutions
Example Question #3 : Give Examples Of Linear Equations: Ccss.Math.Content.8.Ee.C.7a
Solve:
First factorize the numerator.
Rewrite the equation.
The 
Subtract one on both sides.
However, let's substitute this answer back to the original equation to check whether if we will get 
Simplify the left side.
The left side does not satisfy the equation because the fraction cannot be divided by zero.
Therefore, 
The answer is:
Example Question #1 : How To Find Out When An Equation Has No Solution
Solve for 
No solution
No solution
Combine like terms on each side of the equation:
Next, subtract 
Then subtract 
This is nonsensical; therefore, there is no solution to the equation.
All Common Core: 8th Grade Math Resources