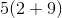Common Core: 6th Grade Math : The Number System
Study concepts, example questions & explanations for Common Core: 6th Grade Math
All Common Core: 6th Grade Math Resources
Example Questions
Example Question #471 : The Number System
Shawn bought two coats at the jacket store for 
In order to find the cost of the coat that Shawn kept you must subtract the amount of money that went back on his credit card from the total that he spent on the two coats.
Example Question #472 : The Number System
Use the distributive property to express the sum 
None of these
The distributive property can be used to rewrite an expression. When we use this property we will identify and pull out the greatest common factor of each of the addends. Then we can create a quantity that represents the sum of two whole numbers with no common factor multiplied by their greatest common factor.
In this case, the greatest common factor shared by each number is:
After we reduce each addend by the greatest common factor we can rewrite the expression:
Example Question #2 : Find Greatest Common Factor
Use the distributive property to express the sum 
The distributive property can be used to rewrite an expression. When we use this property we will identify and pull out the greatest common factor of each of the addends. Then we can create a quantity that represents the sum of two whole numbers with no common factor multiplied by their greatest common factor.
In this case, the greatest common factor shared by each number is:
After we reduce each addend by the greatest common factor we can rewrite the expression:
Example Question #473 : The Number System
Use the distributive property to express the sum 
None of these
The distributive property can be used to rewrite an expression. When we use this property we will identify and pull out the greatest common factor of each of the addends. Then we can create a quantity that represents the sum of two whole numbers with no common factor multiplied by their greatest common factor.
In this case, the greatest common factor shared by each number is:
After we reduce each addend by the greatest common factor we can rewrite the expression:
Example Question #4 : Find Greatest Common Factor
Use the distributive property to express the sum 
The distributive property can be used to rewrite an expression. When we use this property we will identify and pull out the greatest common factor of each of the addends. Then we can create a quantity that represents the sum of two whole numbers with no common factor multiplied by their greatest common factor.
In this case, the greatest common factor shared by each number is:
After we reduce each addend by the greatest common factor we can rewrite the expression:
Example Question #5 : Find Greatest Common Factor
Use the distributive property to express the sum 
None of these
The distributive property can be used to rewrite an expression. When we use this property we will identify and pull out the greatest common factor of each of the addends. Then we can create a quantity that represents the sum of two whole numbers with no common factor multiplied by their greatest common factor.
In this case, the greatest common factor shared by each number is:
After we reduce each addend by the greatest common factor we can rewrite the expression:
Example Question #474 : The Number System
Use the distributive property to express the sum 
The distributive property can be used to rewrite an expression. When we use this property we will identify and pull out the greatest common factor of each of the addends. Then we can create a quantity that represents the sum of two whole numbers with no common factor multiplied by their greatest common factor.
In this case, the greatest common factor shared by each number is:
After we reduce each addend by the greatest common factor we can rewrite the expression:
Example Question #3 : Find Greatest Common Factor And Least Common Multiple: Ccss.Math.Content.6.Ns.B.4
Use the distributive property to express the sum 
None of these
The distributive property can be used to rewrite an expression. When we use this property we will identify and pull out the greatest common factor of each of the addends. Then we can create a quantity that represents the sum of two whole numbers with no common factor multiplied by their greatest common factor.
In this case, the greatest common factor shared by each number is:
After we reduce each addend by the greatest common factor we can rewrite the expression:
Example Question #4 : Find Greatest Common Factor And Least Common Multiple: Ccss.Math.Content.6.Ns.B.4
Use the distributive property to express the sum 
The distributive property can be used to rewrite an expression. When we use this property we will identify and pull out the greatest common factor of each of the addends. Then we can create a quantity that represents the sum of two whole numbers with no common factor multiplied by their greatest common factor.
In this case, the greatest common factor shared by each number is:
After we reduce each addend by the greatest common factor we can rewrite the expression:
Example Question #475 : The Number System
Use the distributive property to express the sum 
None of these
The distributive property can be used to rewrite an expression. When we use this property we will identify and pull out the greatest common factor of each of the addends. Then we can create a quantity that represents the sum of two whole numbers with no common factor multiplied by their greatest common factor.
In this case, the greatest common factor shared by each number is:
After we reduce each addend by the greatest common factor we can rewrite the expression:
All Common Core: 6th Grade Math Resources
