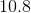All Common Core: 4th Grade Math Resources
Example Questions
Example Question #297 : Number & Operations: Fractions
When we add fractions, we must have common denominators. Whenever we have a number over or we can add (s) to the numerator and denominator to make common denominators.
Example Question #22 : Express A Fraction With Denominator 10 As An Equivalent Fraction With Denominator 100: Ccss.Math.Content.4.Nf.C.5
When we add fractions, we must have common denominators. Whenever we have a number over or we can add (s) to the numerator and denominator to make common denominators.
Example Question #23 : Express A Fraction With Denominator 10 As An Equivalent Fraction With Denominator 100: Ccss.Math.Content.4.Nf.C.5
When we add fractions, we must have common denominators. Whenever we have a number over or we can add (s) to the numerator and denominator to make common denominators.
Example Question #24 : Express A Fraction With Denominator 10 As An Equivalent Fraction With Denominator 100: Ccss.Math.Content.4.Nf.C.5
When we add fractions, we must have common denominators. Whenever we have a number over or we can add (s) to the numerator and denominator to make common denominators.
Example Question #21 : Understand Decimal Notation For Fractions, And Compare Decimal Fractions
What decimal is equivalent to ?
is fifty-seven hundredths.
is fifty-seven hundredths. When we say a decimal, we say the number and add the place-value of the last digit.
Example Question #22 : Understand Decimal Notation For Fractions, And Compare Decimal Fractions
What decimal is equivalent to ?
is sixty-nine hundredths.
is sixty-nine hundredths. When we say a decimal, we say the number and add the place-value of the last digit.
Example Question #1325 : Numbers And Operations
What decimal is equivalent to ?
is eighteen hundredths.
is eighteen hundredths. When we say a decimal, we say the number and add the place-value of the last digit.
Example Question #1991 : Ssat Middle Level Quantitative (Math)
What decimal is equivalent to ?
is seven hundredths.
is seven hundredths. When we say a decimal, we say the number and add the place-value of the last digit.
Example Question #1 : Use Decimal Notation For Fractions With Denominators 10 Or 100: Ccss.Math.Content.4.Nf.C.6
Select the decimal that is equivalent to
is eighty-one hundredths.
is eighty-one hundredths. When we say a decimal, we say the number and add the place-value of the last digit.
Example Question #1991 : Ssat Middle Level Quantitative (Math)
Select the decimal that is equivalent to
is twelve hundredths.
is twelve hundredths. When we say a decimal, we say the number and add the place-value of the last digit.
All Common Core: 4th Grade Math Resources