is the equation for Universal gravitation.

So the fact that we don't actually know any of the numbers doesn't matter. 

What matters is we have the equation 

The masses have a direct proportional relationship with the force. That means that if a mass doubles, the force doubles. 

We can also see that the radius (distance between the masses) has an inverse square relationship with Force. So if we double the radius, we divide the force by 4.

So based on the problem, we triple a mass and double the radius. So we triple the force then divide by 4.

In this question, we're told that an object is hanging by being supported by two ropes. We're asked to find the tension in each rope.

When answering this question, we have to keep in mind all of the forces acting on the object. Since the object isn't moving, there is no net force acting on it. Moreover, we know that its weight acts downward while the tension in the ropes act upwards.

For this question, we're told that an object hanging from a string is released from an initial height and allowed to swing. We're given the maximum velocity, the object's mass, and the length of the string. We're asked to find the maximum tension in the string.

The first step towards solving this problem is to realize that we're dealing with centripetal motion. When the object is released from an initial height, it begins to fall. But as it falls, the string exerts a tension on the mass and causes the mass to travel in a circular motion. Thus, the tension of the string is supplying the centripetal force.

Furthermore, it's important to remember the point at which the object will have maximum velocity. When the object was initially released from some initial height, all of the object's energy was in the form of gravitational potential energy. As it falls, that potential energy is converted into kinetic energy. Once the object reaches the very bottom of its path of motion, all of the potential energy it once had has been converted into kinetic energy at that instant. Since all of the energy is in the form of kinetic energy, and the object's mass remains constant, we know that this must be the point where the maximum velocity occurs.

Thus, we need to analyze the situation when the mass has swung to the very bottom of the path. At this point, the tension is providing an upward force. Moreover, the only downward force acting on the object is its weight due to gravity. The net force resulting from these two will result in the overall centripetal force on the object. We can put this into an equation as follows.

Since we're trying to solve for the tension in the string, we can isolate the  term in the above expression.

To solve this problem, we first need to take into account the forces acting in the vertical direction separately from the forces acting in the horizontal direction.

First, let's start with the vertical direction. Here, the only force force acting downward is the weight of the box. There are two forces acting upwards on the box; one is the normal force and the other is the vertical component of the tension in the rope that is pulling the box. Because the box is not moving in the vertical direction, there is no net force. Thus, the sum of these forces is equal to zero.

Next, let's take a look at the forces acting horizontally on the box. Acting to the right of the box is the horizontal component of the tension in the rope. Acting to the left is the frictional force. Because the box is moving to the right, it must have experienced a net force in this direction. Thus, the sum of these horizontally acting forces will equal a net force.

Now, we can take the expression we obtained for the normal force and substitute it into the expression we obtained for the horizontally acting forces.

Now that we've found an expression for the coefficient of kinetic friction, all we need to do is plug in the values given in the question stem to arrive at the answer.

All of these are identical to a normal force.

This questions requires an understanding of the conversion of gravitational potential energy to potential energy stored in the compression of a spring. The ball's initial potential energy is  where  is the mass of the ball,  is the acceleration due to gravity, and  is the height of the ball. The energy stored in a compressed spring is  where  is the potential energy,  is the spring constant (typically given in ) and  is the compression of the spring. By setting the gravitational potential energy equal to the energy stored in the spring, we can solve for the spring constant :

The new equilibrium position will be where the spring force is opposite in direction and equal in magnitude to the gravitational force on the mass. This occurs where where is the displacement of the spring from equilibrium. Solving for , we get .

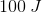
The first step in answering this question is to recognize that we're dealing with two components of a spring; force and energy. Hence, we'll need to utilize both equations. Because both of them share the term for the displacement of the object, that will be the variable that links the two expressions.

Having isolated the variable for displacement, we can plug this value into the force equation.

Now, we can plug in the values given to us in the question stem.

Note that the negative sign shown here indicates the direction of the force. This is because the force is acting in the direction opposite the displacement of the object. Since the question stem asks for the magnitude of force, we don't need to include the negative sign in our answer.

The maximum amount of torque is the magnitude of the torque vector , which is maximized when the angle between the applied force and the displacement vector is 90 degrees. Then the torque is given by , where is the length of the wrench and is the magnitude of the force applied. Since the mechanic doesn't get any stronger, but the handle length increases, the torque doubles.