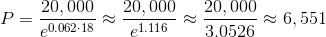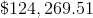We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

College Algebra : Exponential and Logarithmic Functions

Study concepts, example questions & explanations for College Algebra

Create An Account

All College Algebra Resources

5 Diagnostic Tests 84 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 4 5 6 7 8 9 Next →

Example Question #71 : Exponential And Logarithmic Functions

Solve for x:

$log_{2}x=4$

Possible Answers:

x=16

x=2

x=32

x=8

Correct answer:

x=16

Explanation:

In order to solve for x in a logarithmic function, we need to change it into exponential form. That looks as follows:

$log_{b}x=y\rightarrow b^{y}=x$

For this problem, manipulate the log and solve:

$log_{2}x=4$

$2^{4}=x$

x=16

Report an Error

Example Question #72 : Exponential And Logarithmic Functions

Solve for x:

$log_{4}x=2$

Possible Answers:

x=8

x=64

x=16

x=2

Correct answer:

x=16

Explanation:

In order to solve for x in a logarithmic function, we need to change it into exponential form. That looks as follows:

$log_{b}x=y\rightarrow b^{y}=x$

For this problem, manipulate the log and solve:

$log_{4}x=2$

$4^{2}=x$

x=16

Report an Error

Example Question #73 : Exponential And Logarithmic Functions

Solve for x:

$log_{7}x=3$

Possible Answers:

x=343

x=21

x=2187

x=49

Correct answer:

x=343

Explanation:

In order to solve for x in a logarithmic function, we need to change it into exponential form. That looks as follows:

$log_{b}x=y\rightarrow b^{y}=x$

For this problem, manipulate the log and solve:

$log_{7}x=3$

$7^{3}=x$

x=343

Report an Error

Example Question #71 : Exponential And Logarithmic Functions

What is the correct value of ? 3log_b (10)=1

Possible Answers:

log(300)

1000

300

$\frac{1}{1000}$

Correct answer:

1000

Explanation:

Divide by three on both sides.

$\frac{3log_b (10)}{3}=\frac{1}{3}$

$log_b (10)=\frac{1}{3}$

If we would recall 10^2 = 100 and $log_{10}(100) = 2$ , this indicates that:

$b^{\frac{1}{3}} = 10$

Cube both sides to isolate b.

$(b^{\frac{1}{3}}) ^3= 10^3$

The answer is: 1000

Report an Error

Example Question #74 : Exponential And Logarithmic Functions

What is the value of 3log_4(64) ?

Possible Answers:

Correct answer:

Explanation:

The expression can be rewritten as:

$3log_4(64) = 3(\frac{log(64)}{log (4)}) = 3(\frac{log(4^3)}{log(4^1)}) =3(\frac{3log(4)}{log(4)})$

The answer is:

Report an Error

Example Question #75 : Exponential And Logarithmic Functions

Solve this logarithm: $\log_{10} (5x-1)=\log_{10} (x+9)$

Possible Answers:

$x=\frac{1}{5}$

$x=\frac{2}{5}$

None of these

$x=\frac{10}{2}$

$x=\frac{5}{2}$

Correct answer:

$x=\frac{5}{2}$

Explanation:

By the one-to-one property of logarithms we are able to set 5x-1=x+9 and solve.

$5x-1=x+9\rightarrow 5x=x+10\rightarrow 4x=10\rightarrow \boldsymbol{x=\frac{5}{2}}$

Report an Error

Example Question #21 : Solving Logarithmic Functions

Solve the logarithm: $-8-3\ln x=13$

Possible Answers:

$x\approx 3.12 \times 10^{4}$

$x\approx 3.12 \times 10^{-4}$

$x\approx 9.12 \times 10^{-4}$

$x\approx 2.19\times 10^{-4}$

$x\approx 1.92 \times 10^{-4}$

Correct answer:

$x\approx 9.12 \times 10^{-4}$

Explanation:

$-8-3\ln x=13$

add 8 to both sides:

$-3\ln x=21$

divide both sides by -3:

$\ln x=-7$

exponentiate both sides:

$e^{\ln x}=e^{-7}$

$x=\boldsymbol{e^{-7}\approx9.12\times 10^{-4}}$

Report an Error

Example Question #1 : Applications

On the day of a child's birth, a sum of money is to be invested into a certificate of deposit (CD) that draws $6.2\%$ annual interest compounded continuously. The plan is for the value of the CD to be at least $\$20,000$ on the child's $18^{th}$ birthday.

If the amount of money invested is to be a multiple of $\$1,000$ , what is the minimum that should be invested initially, assuming that there are no further deposits or withdrawals?

Possible Answers:

$\$9,000$

$\$10,000$

$\$6,000$

$\$7,000$

$\$8,000$

Correct answer:

$\$7,000$

Explanation:

If we let be the initial amount invested and be the annual interest rate of the CD expressed as a decimal, then at the end of years, the amount of money that the CD will be worth can be determined by the formula

$A = Pe^{rt}$

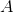
Substitute A = 20,000 , r = 0.062 , t = 18 , and solve for .

$20,000 = Pe^{0.062 \cdot 18}$

$P = \frac{20,000 }{e^{0.062 \cdot 18}} \approx \frac{20,000 }{e^{1.116}} \approx \frac{20,000 }{3.0526} \approx 6,551$

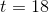
The minimum principal to be invested initially is $6,551. However, since we are looking for the multiple of $1,000 that guarantees a minimum final balance of $20,000, we round up to the nearest such multiple, which is $7,000 - the correct response.

Report an Error

Example Question #3311 : Algebra Ii

Twelve years ago, your grandma put money into a savings account for you that earns $7.5\%$ interest annually and is continuously compounded. How much money is currently in your account if she initially deposited $\$10,000$ and you have not taken any money out?

Possible Answers:

$8,103

$24,596

$81,030

$10,778

$21,170

Correct answer:

$24,596

Explanation:

1. Use $x=Pe^{rt}$ where is the current amount, is the interest rate, is the amount of time in years since the initial deposit, and is the amount initially deposited.

r=0.075

P=$10,000

t=12

2. Solve for

$x=Pe^{rt}$

$x=10,000e^{(0.075\cdot12)}$

x=24,596.03

You currently have $24,596 in your account.

Report an Error

Example Question #76 : College Algebra

Jeffrey has won a lottery and has elected to take a $10,000 per month payment.

At the beginning of the year, Jeffrey deposits the first payment of $10,000 in an account that pays 7.6% interest annually, compounded continuously. At the very beginning of each month, he deposits another $10,000. How much will he have at the very end of the year?

Possible Answers:

$\$125,072.98$

$\$124,269.51$

$\$123,561.85$

$\$124,283.35$

$\$125.056.56$

Correct answer:

$\$125,072.98$

Explanation:

The continuous compound interest formula is

$A= Pe^{rt}$ ,

where is the amount of money in the account at the end of the period, is the principal at the beginning, is the annual interest rate in decimal form, and is the number of years over which the interest accumulates. Since Jeff deposits $1,000 per month, we apply this formula twelve times, with equal to the principal at the beginning of each successive month, r = 0.076 , and $t = \frac{1}{12} \approx 0.08333$ .

We can go ahead and calculate $e^{rt}$ , since and do not change:

$e^{rt}= e^{0.076 \cdot \frac{1}{12}} \approx e^{0.00633 } \approx 1.00635$

The formula can be rewritten as

A= P ( 1.006353)

At the beginning of January, Jeffrey deposits $10,000. At the end of January, there is

$A= \$10,000 ( 1.006353) = \$10,063.53$

in the account.

At the beginning of February, he again deposits $10,000, so there is now

$\$10,063.53+ \$10,000 = \$20,063.53$

in the account.

At the end of February, there is

$A= \$20,063.53 ( 1.006353) = \$ 20,191.01$

in the account.

Repeat addition of $10,000, then multiplication by 1.006353, ten more times to get the amount of money in the account at the end of December. This will be $125,072.98.

Report an Error

← Previous 1 2 3 4 5 6 7 8 9 Next →

View College Algebra Tutors

Odysseas
Certified Tutor

University of New Hampshire at Manchester, Master of Science, Civil Engineering. National Technical University of Athens, Doc...

View College Algebra Tutors

Kayley
Certified Tutor

New Mexico State University-Main Campus, Bachelor of Science, Biology, General.

View College Algebra Tutors

Akunna
Certified Tutor

Bergen Community College, Associate in Science, Natural Sciences. Long Island University-Brooklyn Campus, Current Grad Studen...

All College Algebra Resources

5 Diagnostic Tests 84 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in Chicago, Algebra Tutors in Los Angeles, Chemistry Tutors in San Diego, Spanish Tutors in Los Angeles, English Tutors in Philadelphia, Math Tutors in Denver, Algebra Tutors in Miami, Reading Tutors in Miami, French Tutors in Philadelphia, Chemistry Tutors in Denver

Popular Courses & Classes

MCAT Courses & Classes in San Diego, GMAT Courses & Classes in Boston, GMAT Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Washington DC, ISEE Courses & Classes in Houston, SAT Courses & Classes in Los Angeles, SAT Courses & Classes in New York City, Spanish Courses & Classes in Los Angeles, LSAT Courses & Classes in Philadelphia, ACT Courses & Classes in Denver

Popular Test Prep

LSAT Test Prep in Denver, SSAT Test Prep in Boston, MCAT Test Prep in Washington DC, ISEE Test Prep in Houston, LSAT Test Prep in Los Angeles, GMAT Test Prep in Dallas Fort Worth, LSAT Test Prep in Washington DC, SAT Test Prep in Washington DC, SAT Test Prep in New York City, SSAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

College Algebra : Exponential and Logarithmic Functions

Study concepts, example questions & explanations for College Algebra

All College Algebra Resources

Example Questions

Example Question #71 : Exponential And Logarithmic Functions

Example Question #72 : Exponential And Logarithmic Functions

Example Question #73 : Exponential And Logarithmic Functions

Example Question #71 : Exponential And Logarithmic Functions

Example Question #74 : Exponential And Logarithmic Functions

Example Question #75 : Exponential And Logarithmic Functions

Example Question #21 : Solving Logarithmic Functions

Example Question #1 : Applications

Example Question #3311 : Algebra Ii

Example Question #76 : College Algebra

All College Algebra Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: