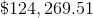College Algebra : Exponential and Logarithmic Functions
Study concepts, example questions & explanations for College Algebra
All College Algebra Resources
Example Questions
Example Question #81 : Exponential And Logarithmic Functions
Sheila has won a lottery and has elected to take a $10,000 per month payment.
At the beginning of the year, Sheila deposits the first payment of $10,000 in an account that pays 7.6% interest annually, compounded monthly. At the very beginning of each month, she deposits another $10,000. How much will she have at the very end of the year?
The periodic compound interest formula is
where 
Since Sheila deposits $1,000 per month, we apply this formula twelve times, with 
We can go ahead and calculate 
The formula can be rewritten as
At the beginning of January, Sheila deposits $10,000. At the end of January, there is
in the account.
At the beginning of February, she again deposits $10,000, so there is now
in the account.
At the end of February, there is
in the account.
Repeat addition of $10,000, then multiplication by 1.006333, ten more times to get the amount of money in the account at the end of December. This will be $125.056.56
Example Question #82 : Exponential And Logarithmic Functions
An investor places $5,000 into an account that has a 5% interest rate. If the he keeps his money in the account for 57 months, and it is compounded quarterly, how much interest will he earn?
Round your answer to the nearest dollar, if needed
Use the formula for compound interest to solve:
"A" is the amount of interest, "P" is the initial amount invested, "r" is the interest rate, "m" is the number of times per year the interest is compounded, and "t" is the number of years the money is invested.
Plug in the appropriate values for the equation:
Because "t" is measure in years, 57 months needs to be converted to years (i.e. 57 months=4.75 years) to solve this equation
Simplify the equation:
Solution:
Certified Tutor
Certified Tutor
All College Algebra Resources
